gmsh手册
Table of Contents
- 1. 第 1 章: Gmsh 概述
- 2. 第二章
- 2.1. 2.1 t1: 几何基础, 基本实体, 物理组
- 2.2. 2.2 t2: 变换, 拉伸几何, 体积
- 2.3. 2.3 t3: 拉伸网格, ONELAB参数, 选项
- 2.4. 2.4 t4: 内置函数, 表面中的孔洞, 标注, 实体颜色
- 2.5. 2.5 t5: 网格尺寸, 宏, 循环, 体积中的孔洞
- 2.6. 2.6 t6: 超限网格, 删除实体
- 2.7. 2.7 t7: 背景网格
- 2.8. 2.8 t8: 后处理, 图像导出和动画
- 2.9. 2.9 t9: 插件
- 2.10. 2.10 t10: 网格尺寸场
- 2.11. 2.11 t11: 非结构化四边形网格
- 2.12. 2.12 t12: 使用复合实体的跨面片网格划分
- 2.13. 2.13 t13: 无需底层CAD模型对STL文件重新划分网格
- 2.14. 2.14 t14: 同调与上同调计算
- 2.15. 2.15 t15: 嵌入的点, 线和面
- 2.16. 2.16 t16: 构造实体几何, OpenCASCADE几何内核
- 2.17. 2.17 t17: 各向异性背景网格
- 2.18. 2.18 t18: 周期性网格
- 2.19. 2.19 t19: 截面体, 倒圆角, 管道, 基于曲率的网格尺寸
- 2.20. 2.20 t20: STEP导入与操作, 几何分区
- 3. 第3章: Gmsh图形用户界面
- 4. 第4章: Gmsh命令行界面
- 5. 第五章: Gmsh脚本语言
- 6. 7 Gmsh 选项
- 7. 8 Gmsh 网格尺寸场
- 7.1. AttractorAnisoCurve
- 7.2. AutomaticMeshSizeField
- 7.3. Ball
- 7.4. BoundaryLayer
- 7.5. Box
- 7.6. Constant
- 7.7. Curvature
- 7.8. Cylinder
- 7.9. Distance
- 7.10. Extend
- 7.11. ExternalProcess
- 7.12. Frustum
- 7.13. Gradient
- 7.14. IntersectAniso
- 7.15. Laplacian
- 7.16. LonLat
- 7.17. MathEval
- 7.18. MathEvalAniso
- 7.19. Max
- 7.20. MaxEigenHessian
- 7.21. Mean
- 7.22. Min
- 7.23. MinAniso
- 7.24. Octree
- 7.25. Param
- 7.26. PostView
- 7.27. Restrict
- 7.28. Structured
- 7.29. Threshold
1. 第 1 章: Gmsh 概述
Gmsh 是一个三维有限元网格生成器, 内置一个 CAD 引擎和后处理器. 其设计目标是提供一个快速, 轻量且用户友好的网格划分工具, 具有参数化输入和灵活的可视化功能.
Gmsh 围绕四个模块构建(几何, 网格, 求解器和后处理), 这些模块可以通过图形用户界面(GUI; 参见第 3 章 [Gmsh 图形用户界面], ), 命令行(参见第 4 章 [Gmsh 命令行界面], ), 使用 Gmsh 自己的脚本语言编写的文本文件('.geo' 文件; 参见第 5 章 [Gmsh 脚本语言]), 或通过 C++, C, Python, Julia 和 Fortran 应用程序编程接口(API; 参见第 6 章 [Gmsh 应用程序编程接口])来控制.
下文将简要介绍这四个模块, 然后概述 Gmsh 的优点(…以及其不足之处), 并提供一些关于如何在您的计算机上安装和运行 Gmsh 的实用信息.
1.1. 1.1 几何模块
Gmsh 中的模型使用其边界表示(Boundary Representation, BRep)来定义: 一个体由一组面界定, 一个面由一系列曲线界定, 一条曲线由两个端点界定. 模型实体是拓扑实体, 即它们只处理模型中的邻接关系, 并实现为一组抽象的拓扑类. 这个 BRep 通过定义嵌入的或内部的模型实体得到扩展: 内部的点, 曲线和面可以嵌入到体中; 内部的点和曲线可以嵌入到面中.
模型实体的几何形状可以由不同的 CAD 内核提供. Gmsh 接口的两个默认内核是内置内核和 OpenCASCADE 内核. Gmsh 不会将几何表示从一个内核转换到另一个内核, 或从这些内核转换到某个中性表示. 相反, Gmsh 直接查询每个 CAD 内核的本机数据, 这避免了数据丢失, 并且对于复杂的模型至关重要, 因为在这些模型中, 转换总是会引入与略有不同的表示相关的问题. 在 .geo 脚本中选择 CAD 内核是通过 SetFactory 命令完成的(参见章节 5.2 [几何脚本命令], ), 而在 Gmsh API 中, 内核在 gmsh/model 命名空间中所有相关函数中显式出现, 分别使用 geo 或 occ 前缀表示内置内核和 OpenCASCADE 内核(参见章节 6.3 [命名空间 gmsh/model], ).
实体既可以使用内置内核和 OpenCASCADE 内核以自下而上的方式构建(首先是点, 然后是曲线, 曲面和体), 也可以使用 OpenCASCADE 内核以自上而下的构造实体几何(Constructive Solid Geometry)方式构建(在实体上执行布尔运算). 这两种方法也可以结合使用. 最后, 可以基于基本的几何实体定义模型实体的组(称为"物理组"). (有关物理组如何影响网格保存方式的更多信息, 请参见章节 1.2.3 [基本实体与物理组],. )
模型实体(也称为"基本实体")和物理组都由一对整数唯一确定: 它们的维度(0 代表点, 1 代表曲线, 2 代表曲面, 3 代表体)和它们的标签, 一个严格为正的全局标识号. 实体和组的标签在每个维度内是唯一的 :
- 每个点必须拥有一个唯一的标签;
- 每条曲线必须拥有一个唯一的标签;
- 每个曲面必须拥有一个唯一的标签;
- 每个体必须拥有一个唯一的标签.
零或负标签由 Gmsh 保留供内部使用.
模型实体可以在几何模块内以多种方式进行操作和转换, 但操作总是直接在其各自的 CAD 内核中执行. 如上所述, 没有通用的内部几何表示: 相反, Gmsh 使用每个 CAD 内核自己的 API 直接对本机几何表示执行操作(平移, 旋转, 交集, 并集, 片段等). 本着同样的设计哲学, 模型可以通过每个 CAD 内核自己的导入机制导入到几何模块中. 例如, 默认情况下, Gmsh 通过 OpenCASCADE 导入 STEP 和 IGES 文件, 这将导致创建具有内部 OpenCASCADE 表示的模型实体. 使用内置 CAD 内核表示的模型可以通过导出为 .geo_unrolled 文件序列化到磁盘, 而使用 OpenCASCADE 内核构建的模型可以序列化为 .brep 或 '.xao' 文件.
第 2 章 [Gmsh 教程], 从章节 2.1 [t1], 开始, 是学习如何使用几何模块的最佳起点: 它包含了基于内置和 OpenCASCADE 内核的从简到繁的示例. 请注意, 几何模块的许多功能都可以在 GUI 中交互式使用(参见第 3 章 [Gmsh 图形用户界面], ), 这也是学习 Gmsh 脚本语言和 API 的好方法, 因为几何模块中的操作会自动将相关命令附加到输入脚本文件中, 并且可以选择性地为 API 支持的语言生成输入(参见 General.ScriptingLanguages 选项; 截至 Gmsh 4.14, 此功能仍在开发中. )
除了由 CAD 内核提供几何形状的 CAD 类型几何实体外, Gmsh 还支持离散模型实体, 这些实体由网格(例如 STL)定义. Gmsh 不对此类离散实体执行几何操作, 但可以通过所谓的"重新参数化"过程为它们配备几何形状¹. 然后, 该参数化用于网格划分, 与 CAD 实体完全相同. 示例请参见章节 2.13 [113].
1.2. 1.2 网格模块
模型的有限元网格是通过各种形状的简单几何元素(在 Gmsh 中: 线, 三角形, 四边形, 四面体, 棱柱, 六面体和金字塔)对其几何形状进行剖分, 其排列方式为: 如果其中两个元素相交, 它们只会在一个面, 一条边或一个节点上相交, 绝不会有其他情况. 这定义了所谓的协调网格(conformal mesh). 网格模块实现了多种算法来自动生成此类网格. 默认情况下, Gmsh 生成的网格被认为是无结构的, 即使它们是以结构化的方式生成的(例如, 通过拉伸). 这意味着网格元素仅由其节点的有序列表完全定义, 并且不假定任何两个元素之间存在预定义的排序关系.
为了保证网格的协调性, 网格生成是自下而上进行的: 首先对曲线进行离散化; 然后使用曲线的网格来对曲面进行网格划分; 接着使用曲面的网格来对体进行网格划分. 在这个过程中, 一个实体的网格仅受其边界网格的约束, 除非较低维度的实体被明确嵌入到较高维度的实体中. 例如, 在三维空间中, 离散化一个曲面的三角形只有在该曲面是一个体的边界的一部分, 或者该曲面已被明确嵌入到该体中时, 才会被强制成为最终 3D 网格中四面体的面. 当两个体共享一个公共曲面时, 这会自动确保网格的协调性. 网格元素根据其底层实体的几何方向进行定向. 每个网格划分步骤都受到网格尺寸场的约束, 该尺寸场规定了网格中元素的期望尺寸. 这个尺寸场可以是均匀的, 由与几何点关联的值指定, 或由通用的网格尺寸场定义(例如, 与到某个边界的距离相关, 或与在另一个网格上定义的任意标量场相关):
Gmsh 的网格模块整合了多个一维, 二维和三维网格划分算法:
- 二维非结构化算法生成三角形和/或四边形(当使用重组命令或选项时). 三维非结构化算法生成四面体, 或四面体和金字塔(当边界网格包含四边形时).
- 二维结构化算法(超限和拉伸)默认生成三角形, 但通过使用重组命令或选项可以获得四边形. 三维结构化算法根据它们所基于的曲面网格的类型, 生成四面体, 六面体, 棱柱和金字塔.
所有网格都可以通过 Mesh.SubdivisionAlgorithm 选项细分以生成完全的四边形或完全的六面体网格(参见章节 7.4 [网格选项]).
1.2.1. 1.2.1 选择正确的非结构化算法
Gmsh 提供了多种二维和三维非结构化算法供选择. 每种算法都有其优缺点.
对于所有二维非结构化算法, 首先使用分治算法²构建一个包含一维网格所有点的 Delaunay 网格. 缺失的边通过边交换³来恢复. 在这一初始步骤之后, 可以应用几种算法来生成最终网格 :
- "Mesh Adapt"算法基于局部网格修改⁴. 该技术利用边交换, 分裂和合并: 长边被分裂, 短边被合并, 如果获得更好的几何构型, 则交换边.
- "Delaunay"算法受 INRIA 的 GAMMA 团队工作的启发⁵. 新点按顺序插入到具有最大无量纲外接圆半径的元素的外心处. 然后使用各向异性 Delaunay 准则重新连接网格.
- "Frontal-Delaunay"算法受 S. Rebay 工作的启发⁶.
- 其他具有特定功能的实验性算法也可用. 特别是, "Frontal-Delaunay for Quads"是"Frontal-Delaunay"算法的一个变体, 旨在生成适合重组的直角三角形⁷; 而"BAMG"允许生成各向异性三角剖分⁸.
对于非常复杂的曲面, "MeshAdapt"算法是最稳健的. 当元素质量很重要时, 应尝试"Frontal-Delaunay"算法. 对于平面曲面的非常大的网格, "Delaunay"算法是最快的; 它通常也比"Frontal-Delaunay"更好地处理复杂的网格尺寸场. 当"Delaunay"或"Frontal-Delaunay"算法失败时, 会自动触发"MeshAdapt". "Automatic"算法对平面曲面使用"Delaunay", 对所有其他曲面使用"MeshAdapt".
- "Delaunay"算法分为三个独立的步骤⁹. 首先, 对模型中所有体的并集进行初始网格划分, 而不在体内部插入点. 然后使用 H. Si 的边界恢复算法 Tetgen/BR 恢复曲面网格. 接着应用二维 Delaunay 算法的三维版本, 在体内部插入点以满足网格尺寸约束.
- "Frontal"算法使用 J. Schoeberl 的 Netgen 算法¹⁰.
- "HXT"算法¹¹是 Delaunay 算法的一种新的高效并行重实现.
- 其他具有特定功能的实验性算法也可用. 特别是, "MMG3D"允许生成各向异性四面体剖分¹².
"Delaunay"算法目前是最稳健的, 并且是唯一支持自动生成带有金字塔的混合网格的算法. 嵌入式模型实体和通用网格尺寸场(参见章节 1.2.2 [指定网格单元尺寸])目前仅由"Delaunay"和"HXT"算法支持.
当 Gmsh 配置了 OpenMP 支持时(参见附录 A [编译源代码], ), 大部分网格划分步骤可以并行执行 :
- 一维和二维网格划分使用粗粒度方法并行化, 即每条曲线(或曲面)是顺序划分的, 但可以同时划分多条曲线(或曲面).
- 使用 HXT 的三维网格划分使用细粒度方法并行化, 即单个体的实际网格划分过程是并行完成的.
线程数可以通过命令行上的 nt 标志(参见第 4 章 [Gmsh 命令行界面]), 或通过 General.NumThreads, Mesh.MaxNumThreads1D, Mesh.MaxNumThreads2D 和 Mesh.MaxNumThreads3D 选项来控制(参见章节 7.1 [通用选项], 和章节 7.4 [网格选项]).
1.2.2. 1.2.2 指定网格单元尺寸
为了确定网格元素的尺寸, Gmsh 局部计算以下各项的最小值:
- 模型边界框的尺寸;
- 如果设置了
Mesh.MeshSizeFromPoints, 则为几何点处指定的网格尺寸; - 如果
Mesh.MeshSizeFromCurvature为正, 则基于曲线和曲面曲率的网格尺寸(指定值为每 \(2\pi\) 弧度的元素数量); - 背景网格尺寸场, 表示为网格尺寸场的组合(参见第 8 章 [Gmsh 网格尺寸场], ):
- Box 场指定一个平行六面体区域内外的尺寸;
- Distance 场根据到模型实体的距离指定尺寸;
- MathEval 场使用显式数学函数指定尺寸;
- PostView 场以标量后处理视图的形式指定一个显式背景网格(参见章节 1.4 [后处理模块], , 和第 10 章 [Gmsh 文件格式], ), 其中节点值代表目标尺寸. 这种方法非常通用, 但它需要一个初始(通常是粗糙的)网格和一种在该网格上计算目标尺寸的方法(通常通过误差估计过程, 例如在网格自适应的迭代过程中);
- Extend 场从给定的边界实体向其包围的曲面或体积内扩展尺寸;
- Min 和 Max 场将尺寸指定为使用其他场计算的尺寸的最小值或最大值;
- 任何逐实体的网格尺寸约束.
使用 Gmsh API, 这个值随后可以通过 C++, C, Python, Julia 或 Fortran 网格尺寸回调函数进一步修改, 该函数通过 gmsh/model/mesh/setSizeCallback 提供(参见章节 6.4 [命名空间 gmsh/model/mesh], ).
然后, 将结果值限制在区间 [\(Mesh.MeshSizeMin\), \(Mesh.MeshSizeMax\)] 内(也可以在命令行上用 -clmin 和 -clmax 提供), 并乘以 \(Mesh.MeshSizeFactor\)(在命令行上是 -clscale).
边界网格尺寸在网格生成过程中会在曲面和/或体积内部进行插值, 具体取决于 Mesh.MeshSizeExtendFromBoundary 的值(所有这些选项的默认值参见章节 7.4 [网格选项], ). 当网格元素尺寸完全由背景网格尺寸场指定时, 通常希望设置
Mesh.MeshSizeFromPoints = 0;
Mesh.MeshSizeFromCurvature = 0;
Mesh.MeshSizeExtendFromBoundary = 0;
以防止由于实体边界上的小网格尺寸而导致的实体内部过度细化.
在所有情况下, 网格都受到结构化网格划分约束(例如超限或拉伸网格)以及任何未配备几何体的离散模型实体的约束(因此在网格生成期间将保留其网格). 曲线上的网格还受到 Mesh.MinLineNodes, Mesh.MinCircleNodes 和 Mesh.MinCurveNodes 选项的约束.
1.2.3. 1.2.3 基本实体 vs. 物理组
将基本的几何实体组合成更有意义的组通常很方便, 例如, 定义一些数学("域", "带诺伊曼条件的边界"), 功能("左翼", "机身")或材料("钢", "碳")属性. 在 Gmsh 的几何模块中, 这种分组是通过定义"物理组"来完成的(参见章节 1.1 [几何模块], ).
默认情况下, 在本机 Gmsh MSH 网格文件格式中(参见第 10 章 [Gmsh 文件格式], ), 以及在大多数其他网格格式中, 如果定义了物理组, 输出网格仅包含那些至少属于一个物理组的元素. (不同的网格文件格式以略有不同的方式处理物理组, 这取决于它们定义组的能力. ) 要保存所有网格元素, 无论是否定义了物理组, 请使用 Mesh.SaveAll 选项(参见章节 7.4 [网格选项], )或在命令行上指定 -save_all. 然而, 在某些格式中(例如 MSH2), 设置 Mesh.SaveAll 会丢弃所有物理组定义.
1.3. 1.3 求解器模块
Gmsh 实现了一个 ONELAB ([http://onelab.info](http://onelab.info)) 服务器, 用于与外部求解器或其他代码(称为"客户端")交换数据. ONELAB 接口允许调用这些客户端, 并让它们共享参数和建模信息.
该实现基于客户端-服务器模型, 有一个服务器端数据库和通过内存或 TCP/IP 套接字通信的本地或远程客户端. 与大多数求解器接口不同, ONELAB 服务器对客户端的任何具体细节(输入文件格式, 语法等)没有任何先验知识. 这是通过在任何模拟之前进行一个分析阶段来实现的, 在此阶段, 客户端被要求将其参数集上传到服务器. 参数集的完整性和一致性问题完全在客户端处理: ONELAB 的作用仅限于数据集中, 修改和重新分发.
使用 Gmsh API, 您可以直接将 Gmsh 嵌入到您的 C++, C, Python, Julia 或 Fortran 求解器中, 使用 ONELAB 进行交互式参数定义和修改, 并动态创建后处理数据. 请参阅 prepro.py, customgui.py 和 customgui.cpp 作为示例.
如果您希望保持代码分离, 您也可以通过提供求解器名称(Solver.Name0, Solver.Name1 等)和可执行文件路径(Solver.Executable0, Solver.Executable1 等)来通过套接字与 Gmsh 通信. 然后可以使用 ONELAB 协议交换参数: 请参阅 utils/solvers 目录中的示例. 以这种方式接口的一个功能齐全的求解器是 GetDP ([https://getdp.info](https://getdp.info)), 这是一个使用混合有限元的通用有限元求解器.
1.4. 1.4 后处理模块
后处理模块可以处理多个标量, 矢量或张量数据集, 以及几何形状和网格. 数据集可以以多种格式提供: 人类可读的"解析"格式(这些只是标准输入脚本的一部分, 但通常放在扩展名为 `.pos` 的单独文件中; 参见章节 5.4 [后处理脚本命令], ), 本机 MSH 文件(ASCII 或二进制文件, 扩展名为 `.msh`; 参见第 10 章 [Gmsh 文件格式], ), 或标准的第三方格式, 如 CGNS 或 MED. 数据集也可以使用 Gmsh API 直接导入(参见章节 6.10 [命名空间 gmsh/view], ). 加载到 Gmsh 后, 标量场可以显示为等值线, 等值面或颜色图, 而矢量场可以表示为三维箭头或位移图. 张量场可以显示为冯·米塞斯(Von-Mises)等效应力, 最小/最大特征值, 特征向量, 椭圆或椭球. (要显示其他分组合, 您可以使用 View.ForceNumComponents 选项; 参见章节 7.6 [后处理选项],. ) 每个数据集连同其可视化选项被称为一个"后处理视图", 或简称为一个"视图". 每个视图都有一个名称, 可以单独操作(每个视图在 GUI 中都有自己的按钮, 并且可以在脚本或 API 中通过其索引或唯一标签引用), 也可以全局操作(参见章节 7.6 [后处理选项], 中的 PostProcessing.Link 选项). 对后处理视图可能的操作包括截面计算, 偏移, 抬升, 边界和分量提取, 颜色图和范围修改, 动画, 矢量图形输出等. 这些操作既可以通过修改后处理选项以非破坏性的方式执行, 也可以在使用后处理插件时导致视图数据的实际修改或新视图的创建(参见第 9 章 [Gmsh 插件], ). 两者都可以在脚本中或通过 API 完全自动化(参见例如, 章节 2.8 [18], , 和章节 2.9 [19], ).
默认情况下, Gmsh 将所有后处理视图视为三维绘图, 即在 3D 空间中绘制标量, 矢量和张量基元(点, 曲线, 三角形, 四面体等). 但 Gmsh 也可以将每个包含标量点的后处理视图表示为二维("X-Y")绘图, 可以是空间导向的或时间导向的 :
- 在' 二维空间' 图中, 标量点的顺序与它们在后处理视图中定义的顺序相同: 二维图的横坐标是点序列定义的曲线的弧长横坐标, 并且只使用与点关联的值绘制一条曲线. 如果存在多个时间步, 每个时间步都会生成一条新曲线;
- 在' 二维时间' 图中, 视图中的每个标量点都会绘制一条曲线, 横坐标是时间步.
1.5. 1.5 Gmsh 的…优点
这是一份 Gmsh 最擅长做的事情的初步列表:
- 借助用户定义的宏, 循环, 条件和包含, 使用内置脚本语言快速描述简单和/或"重复性"的几何体(参见章节 5.1.7 [用户定义的宏], , 章节 5.1.8 [循环和条件], , 以及章节 5.1.9 [其他通用命令], ). 对于更高级的几何体, 使用您选择的语言(C++, C, Python, Julia 或 Fortran)中的 Gmsh API(参见第 6 章 [Gmsh 应用程序编程接口], )带来了更大的灵活性, 唯一的缺点是您需要编译您的代码(对于 C++, C 和 Fortran)或配置和安装解释器(Python 或 Julia)以及 Gmsh. Gmsh 网站上分发了一个二进制软件开发工具包(SDK)以简化此过程(参见章节 1.7 [在您的计算机上安装和运行 Gmsh], );
- 参数化这些几何体. Gmsh 的脚本语言或 Gmsh API 使所有命令和命令参数都能依赖于先前的计算. 使用 OpenCASCADE 几何内核, Gmsh 提供了所有常见的构造实体几何操作的访问权限(参见例如章节 2.16 [116]);
- 从其他 CAD 软件以标准交换格式导入几何体. Gmsh 使用 OpenCASCADE 导入此类文件, 包括来自 STEP 和 IGES 文件的标签和颜色信息(参见例如章节 2.20 [t20], );
- 生成非结构化的一维, 二维和三维单纯形(即使用线段, 三角形和四面体)有限元网格(参见章节 1.2 [网格模块], ), 并对单元尺寸进行精细控制(参见章节 1.2.2 [指定网格单元尺寸], );
- 创建简单的拉伸几何体和网格, 并允许自动将此类结构化网格与非结构化网格耦合(在 3D 中使用一层金字塔形单元);
- 生成符合 CAD 模型几何形状的高阶(曲面)网格. 高阶网格优化工具可以保证此类曲面网格的有效性;
- 通过定义 ONELAB 参数与外部求解器交互, 这些参数在 Gmsh 和求解器之间共享, 并可在 GUI 中轻松修改(参见章节 1.3 [求解器模块], );
- 以多种方式可视化和导出计算结果. Gmsh 可以显示标量, 矢量和张量数据集, 对生成的后处理视图执行各种操作(参见章节 1.4 [后处理模块], ), 可以以多种不同格式导出绘图, 并可以生成复杂的动画(参见例如章节 2.8 [18]);
- 在低端机器和/或没有图形界面的机器上运行. Gmsh 可以带或不带 GUI 进行编译(参见附录 A [编译源代码], ), 所有版本都可以交互式使用, 或直接从命令行使用;
- 配置您偏好的选项. Gmsh 拥有大量配置选项, 可以使用 GUI 交互式设置, 散布在脚本文件中, 通过 API 更改, 在每个用户的配置文件中设置以及在命令行上指定(参见第 7 章 [Gmsh 选项], );
- 并且在各种平台(Windows, macOS 和 Linux)上免费完成以上所有操作(参见 [复制条件])!
1.6. 1.6…以及 Gmsh 的不足之处
以下是 Gmsh 的一些已知弱点:
- Gmsh 不是一个多块网格生成器: 所有由 Gmsh 生成的网格在有限元网格的意义上都是协调的;
- Gmsh 的图形用户界面仅暴露了有限数量的可用功能, 并且界面的许多方面可以得到增强(尤其是操纵器).
- 虽然 Gmsh 可以交互式地创建和操作几何体, 但它绝不是一个高级 CAD 系统的完全替代品.
- Gmsh 使用简单的 OpenGL 1.1 进行图形处理, 没有特定的技巧来处理非常大的网格和后处理数据集(如抽取和自动细节层次, 剔除, 高级透明度等).
- 您对 Gmsh 的抱怨 :-)
如果您有技能和一些空闲时间, 欢迎加入该项目: 我们非常乐意接受任何代码贡献(参见附录 B [开发者信息], ), 以弥补上述(以及所有其他)不足之处!
1.7. 1.7 在您的计算机上安装和运行 Gmsh
Gmsh 既可以作为独立应用程序使用, 也可以作为库使用.
作为独立应用程序, Gmsh 可以通过 GUI 控制(参见第 3 章 [Gmsh 图形用户界面], ), 通过命令行(参见第 4 章 [Gmsh 命令行界面], )和通过 .geo 脚本文件(参见第 5 章 [Gmsh 脚本语言], ). 此外, ONELAB 接口(参见章节 1.3 [求解器模块], )允许通过 Unix 或 TCP/IP 套接字与 Gmsh 应用程序交互. 适用于 Windows, Linux 和 macOS 的 Gmsh 应用程序的二进制版本可以从 [https://gmsh.info/#Download](https://gmsh.info/#Download) 下载. 一些 Linux 发行版也提供了 Gmsh 应用程序. 有关如何从源代码编译 Gmsh 应用程序的说明, 请参见附录 A [编译源代码], .
作为一个库, Gmsh 仍然可以像独立 Gmsh 应用程序一样使用, 但此外它还可以使用 Gmsh API(参见第 6 章 [Gmsh 应用程序编程接口], )嵌入到外部代码中. 该 API 可用于 C++, C, Python, Julia 和 Fortran. 一个适用于 Windows, Linux 和 macOS 的二进制软件开发工具包(SDK), 包含动态 Gmsh 库及相关的头文件和模块文件, 可以从 [https://gmsh.info/#Download](https://gmsh.info/#Download) 下载. Python 用户可以使用
pip install --upgrade gmsh
这将下载二进制 SDK 并将文件安装在适当的系统目录中. 一些 Linux 发行版也提供了 Gmsh SDK. 有关如何从源代码编译动态 Gmsh 库的说明, 请参见附录 A [编译源代码].
2. 第二章
以下教程将逐步介绍新功能, 从第一个教程t1(见2.1节)开始. 相应的文件可在Gmsh发行版的tutorials目录中找到.
.geo文件(例如t1.geo)是用Gmsh的内置脚本语言编写的(见第5章" Gmsh脚本语言" ). 你可以直接用Gmsh应用程序打开它们: 在图形用户界面(见第3章" Gmsh图形用户界面" )中, 使用" File->Open" 菜单并选择例如t1.geo. 或者在命令行中运行
gmsh t1.geo
这将启动图形用户界面, 或者运行
gmsh t1.geo -2
以批处理模式执行2D网格划分(见第4章" Gmsh命令行界面" ). tutorials目录的c++, c, python, julia和fortran子目录包含使用Gmsh API编写的对应语言版本的教程(见第6章" Gmsh应用程序编程接口" ). 运行它们需要Gmsh动态库以及相关的头文件(对于C++和C)或模块(对于Python, Julia和Fortran)(见1.7节" 在计算机上安装和运行Gmsh" ). 每个子目录都包含关于如何运行各支持语言教程的附加信息.
所有以字母" t" 开头的教程都同时提供脚本语言版本和API版本. 以字母" x" 开头的扩展教程介绍了仅通过API可用的功能.
请注意, 除了这些教程外, Gmsh发行版还包含许多其他使用内置脚本语言和API编写的示例: 参见examples和benchmarks.
2.1. 2.1 t1: 几何基础, 基本实体, 物理组
参见t1.geo. 也有C++(t1.cpp), C(t1.c), Python(t1.py), Julia(t1.jl)和Fortran(t1.f90)版本.
// Gmsh GEO教程1
// 几何基础, 基本实体, 物理组
// Gmsh脚本语言中最简单的构造是" 赋值" . 以下命令定义一个新变量" lc" :
lc = 1e-2;
// 这个变量可用于定义Gmsh最简单的" 基本实体" --" 点" . 一个点由一个标签(一个严格为正的整数; 这里是" 1" )唯一标识, 并由四个数字定义:
// 三个坐标(X, Y和Z)以及该点附近的目标网格尺寸(lc):
Point(1) = {0, 0, 0, lc};
// 网格单元尺寸的分布将通过在整个几何中对这些网格尺寸进行插值获得. 另一种指定网格尺寸的方法是使用通用的网格尺寸场(见t10.geo).
// 一种特殊情况是使用背景网格(见t7.geo).
// 如果没有提供目标网格尺寸, 将基于模型的整体大小为模型使用默认的均匀粗略尺寸.
// 我们可以再定义一些点. 所有点都应具有不同的标签:
Point(2) = {.1, 0, 0, lc};
Point(3) = {.1, .3, 0, lc};
Point(4) = {0, .3, 0, lc};
// 曲线是Gmsh的第二种基本实体, 在曲线中, 直线是最简单的. 一条直线由一个标签标识, 并由两个点的标签列表定义. 例如, 在下面的命令中,
// 直线1从点1开始, 到点2结束.
// 注意, 曲线标签与点标签是分开的--因此我们可以将标签" 1" 重用于第一条曲线. 一般来说, Gmsh中的基本实体标签在每个几何维度中必须是唯一的.
Line(1) = {1, 2};
Line(2) = {3, 2};
Line(3) = {3, 4};
Line(4) = {4, 1};
// 第三种基本实体是面. 为了从上面定义的四条曲线中定义一个简单的矩形面, 首先必须定义一个曲线环. 曲线环也由一个标签(在曲线环中唯一)标识,
// 并由一系列相连的曲线的有序列表定义, 每条曲线都关联一个符号(取决于曲线形成环的方向):
Curve Loop(1) = {4, 1, -2, 3};
// 然后我们可以将面定义为曲线环的列表(这里只有一个, 代表外部轮廓, 因为没有孔洞--见t4.geo中的带孔洞面示例):
Plane Surface(1) = {1};
// 在这一步, Gmsh已经知道如何显示矩形面1并对其进行网格划分. 如果我们想将基本几何实体组合成更有意义的组(例如, 定义一些数学属性(" 域" , " 带有诺依曼条件的边界" ),
// 功能属性(" 左机翼" , " 机身" )或材料属性(" 钢" , " 碳纤维" )), 则需要一个可选步骤.
// 在Gmsh中, 这种组被称为" 物理组" . 默认情况下, 如果定义了物理组, Gmsh在输出文件中只会导出至少属于一个物理组的网格单元.
// (要强制Gmsh保存所有单元, 无论它们是否属于物理组, 设置Mesh.SaveAll=1; 或者在命令行中指定-save_all. )
// 物理组也由标签标识, 即严格为正的整数, 每个维度(0D, 1D, 2D或3D)中的标签必须唯一. 物理组也可以被赋予名称.
// 这里我们定义一个物理曲线, 将左侧, 底部和右侧的曲线组合到一个组中(指定标签5); 以及一个名为" 我的面" 的物理面(带有自动标签), 包含几何面1:
Physical Curve(5) = {1, 2, 4};
Physical Surface("My surface") = {1};
// 现在几何已经完成, 你可以
// - 要么用Gmsh打开这个文件, 在" 网格" 模块中选择" 2D" 来创建网格; 然后选择" 保存" 将其以默认格式保存到磁盘(或者使用" 文件->导出" 导出为其他格式);
// - 要么运行gmsh t1.geo -2在命令行中以批处理模式进行网格划分.
// 你也可以取消注释本脚本中的以下行:
//
// Mesh 2;
// Save "t1.msh";
//
// 这将使Gmsh在每次解析文件时都进行网格划分并保存网格. (要从命令行简单解析文件, 可以使用gmsh t1.geo -)
// 默认情况下, Gmsh将网格保存为最新版本的Gmsh网格文件格式(" MSH" 格式). 你可以通过在图形用户界面, 命令行或脚本中指定具有不同扩展名的文件名,
// 将网格保存为其他网格格式. 例如
//
// // Save "t1.unv";
// 将把网格保存为UNV格式. 你也可以将网格保存为旧版本的MSH格式:
//
// - 在图形用户界面中: 打开" 文件->导出" , 输入你的filename.msh, 然后在下拉菜单中选择版本.
// - 在命令行中: 使用-format选项(例如gmsh file.geo -format msh2 -2).
// - 在.geo脚本中: 添加Mesh.MshFileVersion = x.y; 对于任何版本号x.y.
// - 另一种方法是, 你也可以不明确指定格式, 只需选择带有.msh2或.msh4扩展名的文件名.
// 注意, 从Gmsh 3.0开始, 模型可以使用除默认内置内核之外的其他几何内核构建. 通过指定
//
// SetFactory("OpenCASCADE");
//
// .geo文件中的所有后续命令将由OpenCASCADE几何内核而不是内置内核处理. 不同的几何内核具有不同的功能.
// 使用OpenCASCADE时, 无需通过依次定义4个点, 4条曲线和1个曲线环来定义矩形面, 而是可以直接定义矩形面:
//
// Rectangle(2) = {.2, 0, 0, .1, .3};
//
// 可以使用Boundary或CombinedBoundary运算符访问基础曲线和点.
//
// 参见例如t16.geo, t18.geo, t19.geo或t20.geo获取基于OpenCASCADE的完整示例, 以及examples/boolean获取更多示例.
2.2. 2.2 t2: 变换, 拉伸几何, 体积
参见t2.geo. 也有C++(t2.cpp), C(t2.c), Python(t2.py), Julia(t2.jl)和Fortran(t2.f90)版本.
// Gmsh GEO教程2
// 变换, 拉伸几何, 体积
// 我们首先包含之前的教程文件, 以便将其作为本教程的基础. 包含一个文件相当于将其内容复制粘贴过来:
Include "t1.geo";
// 我们可以用与在t1.geo中相同的方式添加新的点和曲线:
Point(5) = {0, .4, 0, lc};
Line(5) = {4, 5};
// Gmsh还提供了变换(平移, 旋转等)基本实体或基本实体副本的工具. 例如, 点5可以向左移动0.02:
Translate {-0.02, 0, 0} { Point{5}; }
// 还可以围绕(0, 0.3, 0)将其进一步旋转-Pi/4(沿z轴旋转):
Rotate {{0,0,1}, {0,0.3,0}, -Pi/4} { Point{5}; }
// 注意, Gmsh中没有单位: 坐标只是数字--由用户赋予它们含义.
// 点3可以被复制并沿y轴平移0.05:
Translate {0, 0.05, 0} { Duplicata{ Point{3}; } }
// 这个命令创建了一个带有自动分配标签的新点. 可以通过将鼠标悬停在该点上, 在图形用户界面中获取这个标签: 在这种情况下, 新点的标签是" 6" .
Line(7) = {3, 6};
Line(8) = {6, 5};
Curve Loop(10) = {5,-8,-7,3};
Plane Surface(11) = {10};
// 为了自动化工作流程, 不必使用图形用户界面获取新创建实体的标签, 可以直接使用变换命令的返回值. 例如, Translate命令
// 返回一个包含被变换实体标签的列表. 让我们使用以下命令将两个面1和11的副本向右平移:
my_new_surfs[] = Translate {0.12, 0, 0} { Duplicata{ Surface{1, 11}; } };
// my_new_surfs[](注意方括号和命令末尾的; )表示一个列表, 其中包含两个新面的标签
// (查看" 工具->消息控制台" 查看消息):
Printf("新面 '%g' 和 '%g'", my_new_surfs[0], my_new_surfs[1]);
// 在Gmsh中, 列表使用方括号定义(mylist[] = {1, 2, 3};)以及访问其元素(myotherlist[] = {mylist[0], mylist[2]}; mythirdlist[] = myotherlist[];),
// 列表索引从0开始. 要获取列表的大小, 请使用#号: len = #mylist[].
// 注意, 也可以使用圆括号代替方括号, 因此我们也可以写myfourthlist() = {mylist(0), mylist(1)};.
// 体积是Gmsh中的第四种基本实体. 与通过定义曲线环来构建面的方式相同, 必须定义面环(即" 壳" )来构建体积.
// 以下体积没有孔洞, 因此仅由一个面环组成:
Point(100) = {0., 0.3, 0.12, lc};
Point(101) = {0.1, 0.3, 0.12, lc};
Point(102) = {0.1, 0.35, 0.12, lc};
xyz[] = Point{5}; // 获取点5的坐标
Point(103) = {xyz[0], xyz[1], 0.12, lc};
Line(110) = {4, 100};
Line(111) = {3, 101};
Line(112) = {6, 102};
Line(113) = {5, 103};
Line(114) = {103, 100};
Line(115) = {100, 101};
Line(116) = {101, 102};
Line(117) = {102, 103};
Curve Loop(118) = {115, -111, 3, 110};
Plane Surface(119) = {118};
Curve Loop(120) = {111, 116, -112, -7};
Plane Surface(121) = {120};
Curve Loop(122) = {112, 117, -113, -8};
Plane Surface(123) = {122};
Curve Loop(124) = {114, -110, 5, 113};
Plane Surface(125) = {124};
Curve Loop(126) = {115, 116, 117, 114};
Plane Surface(127) = {126};
Surface Loop(128) = {127, 119, 121, 123, 125, 11};
Volume(129) = {128};
// 当一个体积可以从一个面拉伸得到时, 通常使用Extrude命令更简单, 而无需手动创建所有点, 曲线和面:
Extrude {0, 0, 0.12} { Surface{my_new_surfs[1]}; }
// 以下命令允许手动为一些新点指定网格尺寸:
MeshSize {103, 105, 109, 102, 28, 24, 6, 5} = lc * 3;
// 最后, 我们将体积129和130组合到一个标签为" 1" , 名称为" The volume" 的物理组中:
Physical Volume("The volume", 1) = {129,130};
// 注意, 如果变换工具便于创建复杂几何, 有时生成" 平面" 几何(具有所有基本实体的显式表示)也是有用的.
//
// 这可以通过" 文件->导出" 并选择" Gmsh Unrolled GEO" 格式来实现, 或者在脚本中添加
//
// Save "file.geo_unrolled";
//
// 也可以通过在命令行中使用gmsh t2.geo -0来实现.
2.3. 2.3 t3: 拉伸网格, ONELAB参数, 选项
参见t3.geo. 也有C++(t3.cpp), Python(t3.py), Julia(t3.jl)和Fortran(t3.f90)版本.
// Gmsh GEO教程3
// 拉伸网格, ONELAB参数, 选项
// 同样, 我们从包含第一个教程开始:
Include "t1.geo";
// 与t2.geo中一样, 我们计划沿z轴进行拉伸. 但在这里, 除了拉伸几何外, 我们还想拉伸2D网格.
// 这可以使用相同的Extrude命令完成, 但要指定元素" 层" (这里是2层, 第一层有8个细分, 第二层有2个细分, 两者的高度都是h/2):
h = 0.1;
Extrude {0,0,h} { Surface{1}; Layers{ {8,2}, {0.5,1} }; }
// 拉伸也可以使用旋转而不是平移来执行, 并且生成的网格可以重组为棱柱(这里我们只使用一层, 有7个细分).
// 所有旋转都由轴方向{0,1,0}, 轴点{-0.1,0,0.1}和旋转角度-Pi/2指定:
Extrude { {0,1,0} , {-0.1,0,0.1} , -Pi/2 } {
Surface{28}; Layers{7}; Recombine;
}
// 使用内置几何内核时, 仅支持角度小于Pi的旋转. 要进行完整的旋转, 需要至少应用3次旋转. OpenCASCADE几何内核没有此限制.
// 注意, 平移{-2*h,0,0}和旋转{1,0,0}, {0,0.15,0.25}, Pi/2也可以组合形成" 扭曲" . 这里角度被指定为ONELAB参数,
// 使用DefineConstant语法. ONELAB参数可以在图形用户界面中交互式修改, 并且可以与连接到同一ONELAB数据库的其他代码交换:
DefineConstant[ angle = {90, Min 0, Max 120, Step 1, Name "Parameters/Twisting angle"} ];
// 详细来说, DefineConstant允许你将ONELAB参数" Parameters/Twisting angle" 的值分配给变量angle. 如果ONELAB数据库中不存在该参数,
// DefineConstant将创建它并分配默认值90. 此外, 如果在调用DefineConstant之前已经定义了变量angle,
// 则DefineConstant调用将被简单跳过. 这允许构建通用的参数化模型, 其参数可以从外部冻结--这些参数不再是" 参数" .
// 此功能的一个有趣用途是与-setnumber name value命令行开关结合使用, 该开关定义一个名为name, 值为value的变量.
// 调用gmsh t3.geo -setnumber angle 30将在DefineConstant之前定义angle, 使t3.geo成为非参数化的
// (" Parameters/Twisting angle" 将不会在ONELAB数据库中创建, 也无法在图形用户界面中修改).
out[] = Extrude { {-2*h,0,0}, {1,0,0} , {0,0.15,0.25} , angle * Pi / 180 } {
Surface{50}; Layers{10}; Recombine;
};
// 在最后这个拉伸命令中, 我们通过使用Extrude命令的返回值(一个列表)以编程方式获取体积编号.
// 这个列表包含拉伸面的" 顶部" (在out[0]中), 新创建的体积(在out[1]中)以及侧面的标签(在out[2], out[3]等中).
// 然后我们可以定义一个新的物理体积(标签101)来组合所有基本体积:
Physical Volume(101) = {1, 2, out[1]};
// 现在我们来更改一些选项......由于所有交互式选项都可以在Gmsh的脚本语言中访问, 例如我们可以使点标签可见,
// 或者直接在输入文件中重新定义一些颜色:
Geometry.PointNumbers = 1;
Geometry.Color.Points = Orange;
General.Color.Text = White;
Mesh.Color.Points = {255, 0, 0};
// 注意, 所有颜色都可以用文字或数字定义, 即Mesh.Color.Points = Red等同于Mesh.Color.Points = {255,0,0};
// 并且注意, 与用户定义的变量一样, 选项既可以用作右侧值也可以用作左侧值, 因此以下命令将把面的颜色设置为与点的颜色相同:
Geometry.Color.Surfaces = Geometry.Color.Points;
// 你可以使用" 帮助->当前选项和工作区" 菜单查看所有选项的当前值. 要将所有选项保存到文件中, 使用" 文件->导出->Gmsh选项" .
// 要将当前选项与当前文件关联, 使用" 文件->保存模型选项" . 要将当前选项保存为所有未来Gmsh会话的默认选项, 使用" 文件->保存选项为默认值" .
2.4. 2.4 t4: 内置函数, 表面中的孔洞, 标注, 实体颜色
参见t4.geo. 也有C++(t4.cpp), Python(t4.py), Julia(t4.jl)和Fortran(t4.f90)版本.
// Gmsh GEO教程4
// 内置函数, 表面中的孔洞, 标注, 实体颜色
// 和往常一样, 我们从定义一些变量开始:
e1 = 4.5 * cm; e2 = 6 * cm / 2; e3 = 5 * cm / 2; cm = 1e-02;
h1 = 5 * cm; h2 = 10 * cm; h3 = 5 * cm; h4 = 2 * cm; h5 = 4.5 * cm; R1 = 1 * cm; R2 = 1.5 * cm; r = 1 * cm; Lc1 = 0.01; Lc2 = 0.003;
// 我们可以使用所有常见的数学函数(注意首字母大写), 以及一些有用的函数, 如Hypot(a, b) := Sqrt(a² + b²):
ccos = (-h5*R1 + e2 * Hypot(h5, Hypot(e2, R1))) / (h5² + e2²);
ssin = Sqrt(1 - ccos²);
// 然后我们使用这些变量定义一些点和线:
Point(1) = {-e1-e2, 0 , 0, Lc1}; Point(2) = {-e1-e2, h1 , 0, Lc1};
Point(3) = {-e3-r , h1 , 0, Lc2}; Point(4) = {-e3-r , h1+r , 0, Lc2}; Point(5) = {-e3 , h1+r , 0, Lc2}; Point(6) = {-e3 , h1+h2, 0, Lc1};
Point(7) = { e3 , h1+h2, 0, Lc1}; Point(8) = { e3 , h1+r , 0, Lc2};
Point(9) = { e3+r , h1+r , 0, Lc2}; Point(10)= { e3+r , h1 , 0, Lc2};
Point(11)= { e1+e2, h1 , 0, Lc1}; Point(12)= { e1+e2, 0 , 0, Lc1}; Point(13)= { e2 , 0 , 0, Lc1};
Point(14)= { R1 / ssin, h5+R1*ccos, 0, Lc2};
Point(15)= { 0 , h5 , 0, Lc2};
Point(16)= {-R1 / ssin, h5+R1*ccos, 0, Lc2};
Point(17)= {-e2 , 0.0 , 0, Lc1};
Point(18)= {-R2 , h1+h3 , 0, Lc2}; Point(19)= {-R2 , h1+h3+h4, 0, Lc2};
Point(20)= { 0 , h1+h3+h4, 0, Lc2}; Point(21)= { R2 , h1+h3+h4, 0, Lc2};
Point(22)= { R2 , h1+h3 , 0, Lc2}; Point(23)= { 0 , h1+h3 , 0, Lc2};
Point(24)= { 0, h1+h3+h4+R2, 0, Lc2}; Point(25)= { 0, h1+h3-R2, 0, Lc2};
Line(1) = {1 , 17};
Line(2) = {17, 16};
// Gmsh提供了除直线之外的其他曲线基元: 样条曲线, B样条曲线, 圆弧, 椭圆弧等. 这里我们定义一个新的圆弧, 从点14开始, 到点16结束, 圆心是点15:
Circle(3) = {14,15,16};
// 注意, 在Gmsh中, 圆弧应始终小于Pi. OpenCASCADE几何内核没有此限制.
// 然后我们可以定义额外的线和圆, 以及一个新的表面:
Line(4) = {14, 13}; Line(5) = {13, 12}; Line(6) = {12, 11}; Line(7) = {11, 10}; Circle(8) = {8, 9, 10}; Line(9) = {8, 7}; Line(10) = {7, 6}; Line(11) = {6, 5}; Line(13) = {3, 2}; Line(14) = {2, 1}; Circle(12) = {3, 4, 5}; Line(15) = {18, 19};
Circle(16) = {21, 20, 24}; Circle(17) = {24, 20, 19}; Circle(18) = {18, 23, 25}; Circle(19) = {25, 23, 22};
Line(20) = {21,22};
Curve Loop(21) = {17, -15, 18, 19, -20, 16};
Plane Surface(22) = {21};
// 但我们仍然需要定义外部表面. 由于这个表面有一个孔洞, 它的定义现在需要两个曲线环:
Curve Loop(23) = {11, -12, 13, 14, 1, 2, -3, 4, 5, 6, 7, -8, 9, 10};
Plane Surface(24) = {23, 21};
// 一般规则是, 如果一个表面有N个孔洞, 它由N+1个曲线环定义: 第一个环定义外部边界; 其他环定义孔洞的边界.
// 最后, 我们可以通过嵌入一个包含一些字符串的后处理视图来添加一些注释:
View "comments" {
// 在窗口坐标中添加一个文本字符串, 距离左侧10像素, 距离底部10像素, 使用StrCat函数连接字符串:
T2(10, -10, 0){ StrCat("Created on ", Today, " with Gmsh") };
// 在模型坐标(0, 0.11, 0)处居中添加一个文本字符串:
T3(0, 0.11, 0, TextAttributes("Align", "Center", "Font", "Helvetica")){
"Hole"
};
// 如果一个字符串以'file://'开头, 其余部分被解释为图像文件. 对于3D标注, 模型坐标中的大小可以在@符号后以'widthxheight'的形式指定
//(如果width或height中的一个为0, 则使用自然缩放; 如果两者都为0, 则使用图像的原始像素尺寸):
T3(0, 0.09, 0, TextAttributes("Align", "Center")){
"file://t4_image.png@0.01x0"
};
// 图像的3D方向可以通过在模型空间中指定图像底部和左侧边缘的方向来指定:
T3(-0.01, 0.09, 0, 0){ "file://t4_image.png@0.01x0,0,0,1,0,1,0" };
// 图像也可以以" 广告牌" 模式绘制, 即始终与相机平行, 通过使用#符号:
T3(0, 0.12, 0, TextAttributes("Align", "Center")){
"file://t4_image.png@0.01x0#"
};
// 2D标注的大小直接以像素给出:
T2(350, -7, 0){ "file://t4_image.png@20x0" };
};
// 这个后处理视图采用" 解析" 格式, 即使用与.geo文件相同的解析器进行解释. 对于包含在网格上定义的实际场值的大型后处理数据集,
// 你应该使用MSH文件格式, 它允许高效存储连续或不连续的标量, 矢量和张量场, 或任意多项式阶数.
// 视图和几何实体可以响应双击事件, 这里是向控制台打印一些消息:
View[0].DoubleClickedCommand = "Printf(' View[0] has been double-clicked!' );";
Geometry.DoubleClickedCurveCommand = "Printf(' Curve %g has been double-clicked!' , Geometry.DoubleClickedEntityTag);";
// 我们也可以更改一些实体的颜色:
Color Grey50{ Surface{ 22 }; }
Color Purple{ Surface{ 24 }; }
Color Red{ Curve{ 1:14 }; }
Color Yellow{ Curve{ 15:20 }; }
2.5. 2.5 t5: 网格尺寸, 宏, 循环, 体积中的孔洞
参见t5.geo. 也有C++(t5.cpp), Python(t5.py), Julia(t5.jl)和Fortran(t5.f90)版本.
// Gmsh GEO教程5
// 网格尺寸, 宏, 循环, 体积中的孔洞
// 我们从定义一些目标网格尺寸开始:
lcar1 = .1;
lcar2 = .0005;
lcar3 = .055;
// 如果我们想全局更改这些网格尺寸(不修改上述定义), 我们可以在命令行上使用-clscale选项(或在选项文件中使用Mesh.MeshSizeFactor)给出所有网格尺寸的全局缩放因子. 例如, 使用:
//
// > gmsh t5.geo -clscale 1
//
// 这个输入文件生成一个大约有3000个节点和14,000个四面体的网格. 使用
//
// > gmsh t5.geo -clscale 0.2
//
// 网格大约有231,000个节点和1,360,000个四面体. 你可以在图形用户界面中使用" 工具->统计信息" 菜单检查网格统计信息.
//
// 有关网格尺寸的更多信息, 请参见t10.geo.
// 我们继续定义一些描述截角立方体的基本实体:
Point(1) = {0.5,0.5,0.5,lcar2}; Point(2) = {0.5,0.5,0,lcar1};
Point(3) = {0,0.5,0.5,lcar1}; Point(4) = {0,0,0.5,lcar1};
Point(5) = {0.5,0,0.5,lcar1}; Point(6) = {0.5,0,0,lcar1};
Point(7) = {0,0.5,0,lcar1}; Point(8) = {0,1,0,lcar1};
Point(9) = {1,1,0,lcar1}; Point(11) = {0,1,1,lcar1}; Point(10) = {0,0,1,lcar1}; Point(12) = {1,1,1,lcar1};
Point(13) = {1,0,1,lcar1}; Point(14) = {1,0,0,lcar1};
Line(1) = {8,9}; Line(4) = {11,8}; Line(2) = {9,12}; Line(5) = {9,14}; Line(3) = {12,11}; Line(6) = {14,13};
Line(7) = {13,12}; Line(10) = {10,4}; Line(11) = {4,5}; Line(8) = {11,10}; Line(9) = {10,13}; Line(12) = {5,6};
Line(13) = {6,2}; Line(16) = {3,7}; Line(19) = {5,1}; Line(14) = {2,1}; Line(17) = {7,2}; Line(20) = {7,8}; Line(15) = {1,3}; Line(21) = {6,14}; Line(18) = {3,4};
Curve Loop(22) = {-11,-19,-15,-18}; Plane Surface(23) = {22};
Curve Loop(24) = {16,17,14,15}; Plane Surface(25) = {24};
Curve Loop(26) = {-17,20,1,5,-21,13}; Plane Surface(27) = {26};
Plane Surface(27) ={26};
Curve Loop(28) = {-4,-1,-2,-3}; Plane Surface(29) = {28};
Curve Loop(30) = {-7,2,-5,-6}; Plane Surface(31) = {30};
Curve Loop(32) = {6,-9,10,11,12,21}; Plane Surface(33) = {32};
Curve Loop(34) = {7,3,8,9}; Plane Surface(35) = {34};
Curve Loop(36) = {-10,18,-16,-20,4,-8}; Plane Surface(37) = {36};
Curve Loop(38) = {-14,-13,-12,19}; Plane Surface(39) = {38};
// 我们现在使用用户定义的宏来在立方体中雕刻一些孔洞, 而不是使用包含的文件:
Macro CheeseHole
// 在以下命令中, 我们使用保留变量名'newp', 它会自动选择一个新的点标签. 与'newp'类似, 特殊变量'newc', 'newcl', 'news', 'newsl'和'newv'分别选择新的曲线,
// 曲线环, 表面, 表面环和体积标签.
//
// 如果Geometry.OldNewReg设置为0, 新标签被选择为每个类别(点, 曲线, 曲线环等)的当前最高标签加1. 默认情况下, 为了向后兼容, Geometry.OldNewReg设置为1,
// 并且只使用两个类别: 一个用于点, 一个用于其他所有类别.
p1 = newp; Point(p1) = {x, y, z, lcar3};
p2 = newp; Point(p2) = {x+r,y, z, lcar3};
p3 = newp; Point(p3) = {x, y+r,z, lcar3};
p4 = newp; Point(p4) = {x, y, z+r,lcar3};
p5 = newp; Point(p5) = {x-r,y, z, lcar3};
p6 = newp; Point(p6) = {x, y-r,z, lcar3}; p7 = newp; Point(p7) = {x, y, z-r,lcar3};
c1 = newc; Circle(c1) = {p2,p1,p7}; c2 = newc; Circle(c2) = {p7,p1,p5}; c3 = newc; Circle(c3) = {p5,p1,p4}; c4 = newc; Circle(c4) = {p4,p1,p2};
c5 = newc; Circle(c5) = {p2,p1,p3}; c6 = newc; Circle(c6) = {p3,p1,p5};
c7 = newc; Circle(c7) = {p5,p1,p6}; c8 = newc; Circle(c8) = {p6,p1,p2}; c9 = newc; Circle(c9) = {p7,p1,p3}; c10 = newc; Circle(c10) = {p3,p1,p4}; c11 = newc; Circle(c11) = {p4,p1,p6}; c12 = newc; Circle(c12) = {p6,p1,p7};
// 我们需要非平面表面来定义球形孔洞. 这里我们使用'Surface', 它可用于边界上有3或4条曲线的表面. 使用内置内核时, 如果所有曲线都是具有相同中心的圆弧,
// 则创建一个球形补丁; 否则使用超限插值. 使用OpenCASCADE内核时, 'Surface'可用于具有任意数量边界曲线的情况, 并将通过它们拟合一个B样条补丁.
l1 = newcl; Curve Loop(l1) = {c5,c10,c4};
l2 = newcl; Curve Loop(l2) = {c9,-c5,c1};
l3 = newcl; Curve Loop(l3) = {c12,-c8,-c1};
l4 = newcl; Curve Loop(l4) = {c8,-c4,c11}; l5 = newcl; Curve Loop(l5) = {-c10,c6,c3};
l6 = newcl; Curve Loop(l6) = {-c11,-c3,c7}; l7 = newcl; Curve Loop(l7) = {-c2,-c7,-c12};
l8 = newcl; Curve Loop(l8) = {-c6,-c9,c2};
s1 = news; Surface(s1) = {l1}; s2 = news; Surface(s2) = {l2};
s3 = news; Surface(s3) = {l3}; s4 = news; Surface(s4) = {l4};
s5 = news; Surface(s5) = {l5};
s6 = news; Surface(s6) = {l6};
s7 = news; Surface(s7) = {l7}; s8 = news; Surface(s8) = {l8};
// 然后我们将表面环标签存储在一个列表中供以后参考(我们需要这些来定义最终的体积):
theloops[t] = newsl; Surface Loop(theloops[t]) = {s1, s2, s3, s4, s5, s6, s7, s8};
thehole = newv;
Volume(thehole) = theloops[t];
Return
// 我们可以使用For循环在立方体中生成五个孔洞:
x = 0; y = 0.75; z = 0; r = 0.09;
For t In {1:5}
x += 0.166; z += 0.166;
// 我们调用'CheeseHole'宏:
Call CheeseHole;
// 我们为每个孔洞定义一个物理体积:
Physical Volume (t) = thehole;
// 我们还在终端上打印一些变量(注意, 由于.geo文件中的所有变量在内部都被视为浮点数, 格式字符串应只包含有效的浮点格式说明符, 如%g, %f, %e等):
Printf("Hole %g (center = {%g,%g,%g}, radius = %g) has number %g!", t, x, y, z, r, thehole);
EndFor
// 然后我们可以定义立方体外表面的表面环:
theloops[0] = newreg; Surface Loop(theloops[0]) = {23:39:2};
// 立方体的体积(不包括5个孔洞)现在由6个表面环定义: 第一个表面环定义外表面; 除第一个之外的表面环定义孔洞.
//(同样, 要引用变量数组, 其标识符后跟方括号):
Volume(186) = {theloops[]};
// 注意, 使用OpenCASCADE几何内核的实体建模, 相同的几何可以用完全不同的方式构建: 参见t16.geo.
// 最后, 我们为离散化立方体(不包括孔洞)的元素定义一个物理体积(在For循环中已经为孔洞创建了物理组):
Physical Volume (10) = 186;
// 我们可以只使模型的一部分可见, 只对这个子集进行网格划分:
//
// Hide {:}
// Recursive Show { Volume{129}; }
// Mesh.MeshOnlyVisible=1;
// 可以使用选项全局更改网格算法:
Mesh.Algorithm = 6; // 用于2D网格的Frontal-Delaunay算法
// 它们也可以为单个表面设置, 例如
MeshAlgorithm Surface {31, 35} = 1; // 表面31和35上的MeshAdapt算法
// 要生成曲线网格并对其进行优化以产生可证明有效的曲线元素(参见A. Johnen, J.-F. Remacle和C. Geuzaine. Geometric validity of curvilinear finite elements.
// Journal of Computational Physics 233, pp. 359-372, 2013; 以及T. Toulorge, C. Geuzaine, J.-F. Remacle, J. Lambrechts.
// Robust untangling of curvilinear meshes. Journal of Computational Physics 254, pp. 8-26, 2013), 你可以取消注释以下行:
//
// Mesh.ElementOrder = 2;
// Mesh.HighOrderOptimize = 2;
2.6. 2.6 t6: 超限网格, 删除实体
参见t6.geo. 也有C++(t6.cpp), C(t6.c), Python(t6.py), Julia(t6.jl)和Fortran(t6.f90)版本.
// Gmsh GEO教程6
// 超限网格, 删除实体
// 让我们使用第一个教程中的几何作为本教程的基础:
lc = 1e-2;
Point(1) = {0, 0, 0, lc}; Point(2) = {.1, 0, 0, lc};
Point(3) = {.1, .3, 0, lc};
Point(4) = {0, .3, 0, lc};
Line(1) = {1, 2}; Line(2) = {3, 2}; Line(3) = {3, 4};
Line(4) = {4, 1};
Curve Loop(1) = {4, 1, -2, 3};
Plane Surface(1) = {1};
// 删除表面和左侧的线, 并将该线替换为3条新线:
Delete{ Surface{1}; Curve{4}; }
p1 = newp; Point(p1) = {-0.05, 0.05, 0, lc}; p2 = newp; Point(p2) = {-0.05, 0.1, 0, lc};
l1 = newc; Line(l1) = {1, p1}; l2 = newc; Line(l2) = {p1, p2}; l3 = newc; Line(l3) = {p2, 4};
// 创建一个表面:
Curve Loop(2) = {2, -1, l1, l2, l3, -3};
Plane Surface(1) = {-2};
// " 超限曲线" 网格约束明确指定曲线上节点的位置. 例如, 以下命令强制在曲线2上均匀放置20个节点(包括两个端点上的节点):
Transfinite Curve{2} = 20;
// 让我们在曲线l1, l2和l3的组合上总共放置20个点(注意点p1和p2由曲线共享, 所以我们不会创建6 + 6 + 10 = 22个节点, 而是20个! )
Transfinite Curve{l1} = 6;
Transfinite Curve{l2} = 6;
Transfinite Curve{l3} = 10;
// 最后, 我们在曲线1(反向)和曲线3上按照几何级数放置30个节点:
Transfinite Curve{-1, 3} = 30 Using Progression 1.2;
// " 超限表面" 网格约束在表面的参数平面中使用超限插值算法, 通过结构化网格连接边界上的节点. 如果表面的边界上有超过4个角点,
// 必须手动指定超限插值的角点:
Transfinite Surface{1} = {1, 2, 3, 4};
// 要创建四边形而不是三角形, 可以使用'Recombine'命令:
Recombine Surface{1};
// 当表面的边界上只有3或4个点时, 'Transfinite Surface'约束中可以省略角点列表:
Point(7) = {0.2, 0.2, 0, 1.0};
Point(8) = {0.2, 0.1, 0, 1.0}; Point(9) = {0.25, 0.2, 0, 1.0}; Point(10) = {0.3, 0.1, 0, 1.0};
Line(10) = {8, 10};
Line(11) = {10, 9}; Line(12) = {9, 7};
Line(13) = {7, 8};
Curve Loop(14) = {10, 11, 12, 13};
Plane Surface(15) = {14};
Transfinite Curve {10, 11, 12, 13} = 10;
Transfinite Surface{15};
// 三角形的生成方式可以通过在'Transfinite Surface'命令后附加"Left", "Right"或"Alternate"来控制. 尝试例如
//
// Transfinite Surface{15} Alternate;
// 最后, 我们对网格应用椭圆平滑器以获得更规则的网格:
Mesh.Smoothing = 100;
2.7. 2.7 t7: 背景网格
参见t7.geo. 也有C++(t7.cpp), Python(t7.py), Julia(t7.jl)和Fortran(t7.f90)版本.
// Gmsh GEO教程7 // 背景网格 // 通过提供背景网格(即包含目标网格尺寸的后处理视图), 可以非常精确地指定网格尺寸. // 合并一个包含目标网格尺寸的基于列表的后处理视图: Merge "t7_bgmesh.pos"; // 如果后处理视图是基于模型的而不是基于列表的(即它基于实际网格), 我们需要创建一个新模型来包含几何, 以便对其进行网格划分不会破坏背景网格. // 这里不需要, 因为视图是基于列表的, 但这样做没有坏处: NewModel; // 合并第一个教程的几何: Merge "t1.geo"; // 将该视图应用为当前背景网格尺寸场: Background Mesh View[0]; // 为了仅从背景网格计算网格尺寸, 而忽略任何其他尺寸约束, 可以设置: Mesh.MeshSizeExtendFromBoundary = 0; Mesh.MeshSizeFromPoints = 0; Mesh.MeshSizeFromCurvature = 0; // 参见t10.geo获取更多信息: 背景网格实际上是一般" 网格尺寸场" 的一种特殊情况.
2.8. 2.8 t8: 后处理, 图像导出和动画
参见t8.geo. 也有C++(t8.cpp), Python(t8.py), Julia(t8.jl)和Fortran(t8.f90)版本.
// Gmsh GEO教程8
// 后处理, 图像导出和动画
// 除了创建几何和网格外, GEO脚本还可用于操作后处理数据集(在Gmsh中称为" 视图" ).
// 我们首先包含t1.geo以及一些后处理视图:
Include "t1.geo";
Include "view1.pos"; Include "view1.pos";
Include "view4.pos";
// Gmsh可以读取各种格式的后处理视图. 这里view1.pos和view4.pos文件采用Gmsh" 解析" 格式,
// 由GEO脚本解析器直接解释. 当然, 解析格式应该只用于相对较小的数据集: 对于较大的数据集, 使用例如MSH文件要高效得多.
// 然后我们设置一些通用选项:
General.Trackball = 0;
General.RotationX = 0; General.RotationY = 0; General.RotationZ = 0;
General.Color.Background = White; General.Color.Foreground = Black; General.Color.Text = Black;
General.Orthographic = 0; General.Axes = 0; General.SmallAxes = 0;
// 我们还为每个后处理视图设置一些选项:
v0 = PostProcessing.NbViews-4;
v1 = v0+1; v2 = v0+2; v3 = v0+3;
View[v0].IntervalsType = 2; View[v0].OffsetZ = 0.05; View[v0].RaiseZ = 0; View[v0].Light = 1; View[v0].ShowScale = 0;
View[v0].SmoothNormals = 1;
View[v1].IntervalsType = 1;
View[v1].ColorTable = { Green, Blue };
View[v1].NbIso = 10; View[v1].ShowScale = 0;
View[v2].Name = "Test...";
View[v2].Axes = 1;
View[v2].Color.Axes = Black;
View[v2].IntervalsType = 2; View[v2].Type = 2;
View[v2].AutoPosition = 0; View[v2].PositionX = 85;
View[v2].PositionY = 50; View[v2].Width = 200;
View[v2].Height = 130;
View[v3].Visible = 0;
// 你可以通过在图形用户界面中选择" 文件->导出" 直接保存MPEG电影. 有几个预定义的动画设置, 用于循环视图中的所有时间步, 或在视图之间循环.
// 但是脚本可用于构建更复杂的动画, 通过在运行时更改选项并重新渲染图形. 然后每个帧可以保存到磁盘作为图像, 多个帧可以编码形成电影.
// 下面是这样一个自定义动画的示例.
t = 0; // 初始步骤
// 从1到3循环num
For num In {1:3}
View[v0].TimeStep = t; // 设置时间步
View[v1].TimeStep = t;
View[v2].TimeStep = t;
View[v3].TimeStep = t;
t = (View[v0].TimeStep < View[v0].NbTimeStep-1) ? t+1 : 0; // 递增
View[v0].RaiseZ += 0.01/View[v0].Max * t; // 提升视图v0
If (num == 3) // 当num == 3时调整图形大小, 创建640x480的帧
General.GraphicsWidth = General.MenuWidth + 640;
General.GraphicsHeight = 480;
EndIf
frames = 50;
// 从1到frames循环num2
For num2 In {1:frames}
// 逐步旋转场景
General.RotationX += 10;
General.RotationY = General.RotationX / 3;
General.RotationZ += 0.1;
// 休眠0.01秒
Sleep 0.01;
// 绘制场景(可以使用'DrawForceChanged'代替以强制重建顶点数组, 例如在更改元素裁剪时)
Draw;
If(num == 3) // 取消以下行的注释以将每个帧保存为图像文件('Print'命令保存图形窗口; 'Sprintf'函数允许动态创建文件名):
// Print Sprintf("t8-%g.gif", num2);
// Print Sprintf("t8-%g.ppm", num2);
// Print Sprintf("t8-%g.jpg", num2);
EndIf
EndFor
If(num == 3) // ffmpeg:
// 这里我们可以调用系统命令生成电影. 例如, 使用
// System "ffmpeg -i t8-%d.jpg t8.mpg"
EndIf
EndFor
2.9. 2.9 t9: 插件
参见t9.geo. 也有C++(t9.cpp), Python(t9.py), Julia(t9.jl)和Fortran(t9.f90)版本.
// Gmsh GEO教程9 // 插件 // 插件可以添加到Gmsh中以扩展其功能. 例如, 后处理插件可以修改视图, 或基于先前加载的视图创建新视图. // 几个默认插件与Gmsh静态链接, 例如Isosurface, CutPlane, CutSphere, Skin, Transform或Smooth. // 插件可以与其他选项以相同的方式控制: 要么从图形界面(右键单击视图按钮, 然后选择'Plugins'), 要么从命令文件. // 例如, 让我们包含一个三维标量视图: Include "view3.pos" ; // 然后我们为'Isosurface'插件设置一些选项(从3D标量视图提取等值面), 并运行它: Plugin(Isosurface).Value = 0.67 ; // 等值级别 Plugin(Isosurface).View = 0 ; // 源视图是View[0] Plugin(Isosurface).Run ; // 运行插件! // 我们还为'CutPlane'插件设置一些选项(使用平面A*x+B*y+C*z+D=0计算3D视图的截面), 然后运行它: Plugin(CutPlane).A = 0 ; Plugin(CutPlane).B = 0.2 ; Plugin(CutPlane).C = 1 ; Plugin(CutPlane).D = 0 ; Plugin(CutPlane).View = 0 ; Plugin(CutPlane).Run ; // 添加一个标题(按照惯例, 对于窗口坐标, 大于99999的值表示中心. 我们也可以使用'General.GraphicsWidth / 2', 但这只在当前窗口大小下使字符串居中): Plugin(Annotate).Text = "A nice title" ; Plugin(Annotate).X = 1.e5; Plugin(Annotate).Y = 50 ; Plugin(Annotate).Font = "Times-BoldItalic" ; Plugin(Annotate).FontSize = 28 ; Plugin(Annotate).Align = "Center" ; Plugin(Annotate).View = 0 ; Plugin(Annotate).Run ; Plugin(Annotate).Text = "(and a small subtitle)" ; Plugin(Annotate).Y = 70 ; Plugin(Annotate).Font = "Times-Roman" ; Plugin(Annotate).FontSize = 12 ; Plugin(Annotate).Run ; // 我们最后设置一些选项: View[0].Light = 1; View[0].IntervalsType = 1; View[0].NbIso = 6; View[0].SmoothNormals = 1; View[1].IntervalsType = 2; View[2].IntervalsType = 2;
2.10. 2.10 t10: 网格尺寸场
参见t10.geo. 也有C++(t10.cpp), Python(t10.py), Julia(t10.jl)和Fortran(t10.f90)版本.
// Gmsh GEO教程10
// 网格尺寸场
// 除了在几何的点上指定目标网格尺寸(参见t1.geo)或使用背景网格(参见t7.geo)外, 你还可以使用通用的网格尺寸" 场" .
// 让我们创建一个简单的矩形几何
lc = .15;
Point(1) = {0.0,0.0,0,lc}; Point(2) = {1,0.0,0,lc};
Point(3) = {1,1,0,lc}; Point(4) = {0,1,0,lc};
Point(5) = {0.2,.5,0,lc};
Line(1) = {1,2}; Line(2) = {2,3}; Line(3) = {3,4}; Line(4) = {4,1};
Curve Loop(5) = {1,2,3,4}; Plane Surface(6) = {5};
// 假设我们希望在曲线2和点5附近获得lc/30的网格元素尺寸, 在其他地方获得lc的尺寸. 为了实现这一点, 我们可以使用两个场:
// " Distance" 和" Threshold" . 我们首先在点5和曲线2上定义一个Distance场(Field[1]).
// 这个场返回到点5和(曲线上的100个等距点)曲线2的距离.
Field[1] = Distance;
Field[1].PointsList = {5};
Field[1].CurvesList = {2};
Field[1].Sampling = 100;
// 然后我们定义一个'Threshold'场, 它使用'Distance'场1的返回值来根据计算的距离定义元素尺寸的简单变化
//
// SizeMax -
//
// SizeMin -o----------------/
// Point DistMin DistMax
Field[2] = Threshold;
Field[2].InField = 1;
Field[2].SizeMin = lc / 30;
Field[2].SizeMax = lc;
Field[2].DistMin = 0.15;
Field[2].DistMax = 0.5;
// 假设我们想使用空间坐标的数学函数来调整网格元素尺寸. 我们可以使用MathEval场来做到这一点:
Field[3] = MathEval;
Field[3].F = "cos(4*3.14*x) * sin(4*3.14*y) / 10 + 0.101";
// 我们也可以将MathEval与来自其他场的值结合起来. 例如, 让我们围绕点1定义一个'Distance'场
Field[4] = Distance;
Field[4].PointsList = {1};
// 然后我们可以创建一个'MathEval'场, 其函数依赖于'Distance'场4的返回值, 即取决于到点1的距离
//(这里使用三次定律, 最小元素尺寸= lc / 100)
Field[5] = MathEval;
Field[5].F = Sprintf("F4^3 + %g", lc / 100);
// 我们也可以使用'Box'场在盒子内部施加元素尺寸的阶跃变化
Field[6] = Box;
Field[6].VIn = lc / 15;
Field[6].VOut = lc;
Field[6].XMin = 0.3;
Field[6].XMax = 0.6;
Field[6].YMin = 0.3;
Field[6].YMax = 0.6;
Field[6].Thickness = 0.3;
// 还有许多其他类型的场可用: 参见参考手册获取完整列表. 你也可以直接在图形用户界面中通过在" 网格" 模块中选择" 定义->尺寸场" 来创建场.
// 让我们使用所有场的最小值作为背景网格尺寸场
Field[7] = Min;
Field[7].FieldsList = {2, 3, 5, 6};
Background Field = 7;
// 为了确定网格元素的尺寸, Gmsh在本地计算以下各项的最小值
//
// 1) 模型边界框的尺寸;
// 2) 如果设置了'Mesh.MeshSizeFromPoints', 则为在几何点上指定的网格尺寸;
// 3) 如果'Mesh.MeshSizeFromCurvature'为正数, 则为基于曲率的网格尺寸(该值指定每2*pi弧度的元素数量);
// 4) 背景网格尺寸场;
// 5) 任何每个实体的网格尺寸约束.
//
// 然后该值被约束在[Mesh.MeshSizeMin, Mesh.MeshSizeMax]区间内, 并乘以Mesh.MeshSizeFactor. 此外,
// 边界网格尺寸根据Mesh.MeshSizeExtendFromBoundary的值在表面和/或体积内部进行插值(默认值见相关设置).
//
// 当元素尺寸完全由网格尺寸场指定时(如本例所示), 通常希望设置
Mesh.MeshSizeExtendFromBoundary = 0;
Mesh.MeshSizeFromPoints = 0;
Mesh.MeshSizeFromCurvature = 0;
// 这将防止由于边界上的小网格尺寸而导致过度细化.
// 最后, 虽然默认的"Frontal-Delaunay"2D网格算法(Mesh.Algorithm = 6)通常会生成最高质量的网格,
// 但"Delaunay"算法(Mesh.Algorithm = 5)将更好地处理复杂的网格尺寸场--特别是具有大元素尺寸梯度的尺寸场:
Mesh.Algorithm = 5;
2.11. 2.11 t11: 非结构化四边形网格
参见t11.geo. 也有C++(t11.cpp), Python(t11.py), Julia(t11.jl)和Fortran(t11.f90)版本.
// Gmsh GEO教程11
// 非结构化四边形网格
// 在教程t3.geo和t6.geo中, 我们已经看到通过使用" Recombine" 关键字, 拉伸和超限网格可以" 重组" 为四边形, 棱柱或六面体. 非结构化网格也可以以相同的方式重组.
// 让我们定义一个带有解析网格尺寸场的简单几何:
Point(1) = {-1.25, -.5, 0}; Point(2) = {1.25, -.5, 0};
Point(3) = {1.25, 1.25, 0}; Point(4) = {-1.25, 1.25, 0};
Line(1) = {1, 2}; Line(2) = {2, 3};
Line(3) = {3, 4}; Line(4) = {4, 1};
Curve Loop(4) = {1, 2, 3, 4}; Plane Surface(100) = {4};
Field[1] = MathEval;
Field[1].F = "0.01*(1.0+30.*(y-x*x)*(y-x*x) + (1-x)*(1-x))";
Background Field = 1;
// 要生成四边形而不是三角形, 我们只需添加
Recombine Surface{100};
// 如果我们有多个表面, 可以使用'Recombine Surface {:};'. 另一种方法是指定全局选项"Mesh.RecombineAll = 1;".
// 默认的重组算法称为" Blossom" : 它使用最小成本完美匹配算法从三角剖分生成全四边形网格. 关于该算法的更多细节可以在以下论文中找到:
// J.-F. Remacle, J. Lambrechts, B. Seny, E. Marchandise, A. Johnen and C. Geuzaine, "Blossom-Quad: a non-uniform quadrilateral mesh generator using a minimum cost perfect matching algorithm",
// International Journal for Numerical Methods in Engineering 89, pp. 1102-1119, 2012.
// 对于更好的2D(平面)四边形网格, 你可以尝试实验性的" Frontal-Delaunay for quads" 网格算法, 这是一种三角剖分算法, 能够在几乎所有地方创建直角三角形:
// J.-F. Remacle, F. Henrotte, T. Carrier-Baudouin, E. Bechet, E. Marchandise, C. Geuzaine and T. Mouton. A frontal Delaunay quad mesh generator using the L^inf norm.
// International Journal for Numerical Methods in Engineering, 94, pp. 494-512, 2013.
// 取消以下行的注释以尝试用于四边形的Frontal-Delaunay算法:
// Mesh.Algorithm = 8;
// 如果重组所有三角形会导致形状不佳的四边形, 默认的重组算法可能会在网格中留下一些三角形. 在这种情况下, 要生成全四边形网格,
// 你可以细分得到的混合网格(使用Mesh.SubdivisionAlgorithm = 1), 或者使用全四边形重组算法,
// 它将自动执行更粗的网格, 然后进行重组, 平滑和细分. 取消以下行的注释以尝试全四边形算法:
// Mesh.RecombinationAlgorithm = 2; // 或3
// 注意, 你也可以在网格划分后显式应用重组算法和/或细分步骤, 如下所示:
// Mesh 2;
// RecombineMesh;
// Mesh.SubdivisionAlgorithm = 1;
// RefineMesh;
2.12. 2.12 t12: 使用复合实体的跨面片网格划分
参见t12.geo. 也有C++(t12.cpp), Python(t12.py), Julia(t12.jl)和Fortran(t12.f90)版本.
// Gmsh GEO教程12
// 使用复合实体的跨面片网格划分
// " 复合" 网格约束允许跨表面边界生成网格, 这在例如导入的CAD模型(如STEP)具有不需要的小特征时非常有用.
// 当给出" 复合曲线" 或" 复合表面" 网格约束时, 在网格生成时, Gmsh会:
// 1. 分别对基础基本几何实体进行网格划分;
// 2. 创建一个组合所有单个网格的离散实体;
// 3. 在这个离散实体上计算离散参数化(即分段线性映射);
// 4. 使用这个离散参数化而不是构成复合实体的基础基本实体的基础几何描述对离散实体进行网格划分;
// 5. 可选地, 在原始实体上重新分类网格元素和节点.
// 上面的步骤3只有在组合单个网格得到的网格可以重新参数化时才能执行, 即形状" 足够简单" . 如果形状不适合重新参数化,
// 你应该创建几何的完整网格, 并首先对其进行重新分类以生成适合重新参数化的面片(参见t13.geo).
// 步骤1中执行的单个实体的网格划分通常应该比所需的最终网格更精细; 这可以通过" Mesh.CompoundMeshSizeFactor" 选项控制.
// 步骤5中在基础基本实体上的可选重新分类由" Mesh.CompoundClassify" 选项控制.
lc = 0.1;
Point(1) = {0, 0, 0, lc}; Point(2) = {1, 0, 0, lc};
Point(3) = {1, 1, 0.5, lc}; Point(5) = {0.3, 0.2, 0, lc}; Point(7) = {0, 0.02, 0.02, lc}; Point(8) = {1, 0.05, 0.02, lc}; Point(4) = {0, 1, 0.4, lc}; Point(6) = {0, 0.01, 0.01, lc};
Point(9) = {1, 0.32, 0.02, lc};
Line(1) = {1, 2}; Line(2) = {2, 8}; Line(3) = {8, 9};
Line(4) = {9, 3}; Line(5) = {3, 4}; Line(6) = {4, 7};
Line(7) = {7, 6}; Line(8) = {6, 1}; Spline(9) = {7, 5, 9};
Line(10) = {6, 8};
Curve Loop(11) = {5, 6, 9, 4}; Surface(1) = {11};
Curve Loop(13) = {-9, 3, 10, 7}; Surface(5) = {13};
Curve Loop(15) = {-10, 2, 1, 8}; Surface(10) = {15};
// 将曲线2, 3和4视为单个曲线进行网格划分(即跨点6和7进行网格划分)
Compound Curve{2, 3, 4};
// 对曲线6, 7和8执行同样的操作
Compound Curve{6, 7, 8};
// 将表面1, 5和10视为单个表面进行网格划分(即跨曲线9和10进行网格划分)
Compound Surface{1, 5, 10};
2.13. 2.13 t13: 无需底层CAD模型对STL文件重新划分网格
参见t13.geo. 也有C++(t13.cpp), Python(t13.py), Julia(t13.jl)和Fortran(t13.f90)版本.
// Gmsh GEO教程13
//
// 无需底层CAD模型对STL文件重新划分网格
//
//----
// 我们先合并一个需要重新划分网格的STL网格.
Merge "t13_data.stl";
// 首先, 我们通过沿着尖锐的几何特征分割原始表面, 对表面进行分类(" 着色" ). 这会创建新的离散表面, 曲线和点.
DefineConstant[
// 两个三角形之间的角度超过此值时, 边会被视为尖锐边
angle = {40, Min 20, Max 120, Step 1, Name "Parameters/表面检测角度"},
// 对于复杂几何体, 有些面片可能过于复杂, 细长或过大而难以参数化; 设置以下选项将强制创建可参数化的面片:
forceParametrizablePatches = {0, Choices{0,1}, Name "Parameters/创建保证可参数化的表面"},
// 对于开放表面, 在分类过程中包含边界边:
includeBoundary = 1,
// 强制曲线按给定角度分割:
curveAngle = 180
];
ClassifySurfaces{angle * Pi/180, includeBoundary, forceParametrizablePatches, curveAngle * Pi / 180};
// 为网格中的所有离散曲线和表面创建几何形状, 以便之后可以对它们重新划分网格
CreateGeometry;
// 在批处理模式下, 上述两个步骤可以通过执行" gmsh t13.stl -reparam 40" 来完成, 这会保存包含参数化信息的" t13.msh" , 该文件之后可用于重新划分网格.
// 注意, 如果有CAD模型(例如STEP文件, 参见t20.geo)而不是STL网格, 通常最好使用该CAD模型, 而不是使用通过对网格重新参数化创建的几何. 实际上, CAD几何通常更精确, 参数化更平滑, 能带来更高效, 更高质量的网格划分. Gmsh中的离散表面重新划分网格功能经过优化, 用于处理来自成像系统等没有CAD模型的密集STL网格; 它不太适合处理CAD工具为3D打印等生成的低质量STL三角化网格(这类网格为了减小文件大小而优化, 例如包含非常细长的三角形).
// 像往常一样创建一个体积
Surface Loop(1) = Surface{:};
Volume(1) = {1};
// 我们通过尺寸场来指定单元尺寸, 只是为了演示一下 :-)
funny = DefineNumber[0, Choices{0,1}, Name "Parameters/应用有趣的网格尺寸场? "];
Field[1] = MathEval;
If(funny)
Field[1].F = "2*Sin((x+y)/5) + 3";
Else
Field[1].F = "4";
EndIf
Background Field = 1;
2.14. 2.14 t14: 同调与上同调计算
参见t14.geo. 也有C++(t14.cpp), Python(t14.py), Julia(t14.jl)和Fortran(t14.f90)版本.
// Gmsh GEO教程14
// 同调与上同调计算
//
//
// Gmsh中的同调计算利用模型的网格找到(相对)(上)同调空间基的代表性链. 这些代表性基链作为Gmsh的物理组存储在网格中, 每个链对应一个物理组.
// 创建示例几何
m = 0.5; // 网格尺寸
h = 2; // z方向高度
Point(1) = {0, 0, 0, m};
Point(2) = {10, 0, 0, m};
Point(3) = {10, 10, 0, m};
Point(4) = {0, 10, 0, m};
Point(5) = {4, 4, 0, m};
Point(6) = {6, 4, 0, m};
Point(7) = {6, 6, 0, m};
Point(8) = {4, 6, 0, m};
Point(9) = {2, 0, 0, m};
Point(10) = {8, 0, 0, m};
Point(11) = {2, 10, 0, m};
Point(12) = {8, 10, 0, m};
Line(1) = {1, 9};
Line(2) = {9, 10};
Line(3) = {10, 2};
Line(4) = {2, 3};
Line(5) = {3, 12};
Line(6) = {12, 11};
Line(7) = {11, 4};
Line(8) = {4, 1};
Line(9) = {5, 6};
Line(10) = {6, 7};
Line(11) = {7, 8};
Line(12) = {8, 5};
Curve Loop(13) = {6, 7, 8, 1, 2, 3, 4, 5};
Curve Loop(14) = {11, 12, 9, 10};
Plane Surface(15) = {13, 14};
e() = Extrude {0, 0, h}{ Surface{15}; };
// 创建物理组, 这些物理组用于定义同调计算的域和相对同调计算的子域.
// 整个域
Physical Volume(1) = {e(1)};
// 模型的四个" 终端"
Physical Surface(70) = {e(3)};
Physical Surface(71) = {e(5)};
Physical Surface(72) = {e(7)};
Physical Surface(73) = {e(9)};
// 整个域的表面
bnd() = Abs(Boundary{ Volume{e(1)}; });
Physical Surface(80) = bnd();
// 域表面中除去四个终端的部分
bnd() -= {e(3), e(5), e(7), e(9)};
Physical Surface(75) = bnd();
// 找到域模四个终端的相对同调空间基.
Homology {{1}, {70, 71, 72, 73}};
// 找到与上述基同构的同调空间基: 模非终端域表面的同调空间, 也称为细切割.
Homology {{1}, {75}};
// 找到与上述基同构的上同调空间基: 域模四个终端的上同调空间, 也称为粗切割.
Cohomology {{1}, {70, 71, 72, 73}};
// 更多示例:
// Homology {1};
// Homology;
// Homology {{1}, {80}};
// Homology {{}, {80}};
// 更多信息参见M. Pellikka, S. Suuriniemi, L. Kettunen和C. Geuzaine的<有限元建模中的同调与上同调计算>, 发表于<SIAM Journal on Scientific Computing>35(5), 第1195-1214页, 2013年.
2.15. 2.15 t15: 嵌入的点, 线和面
参见t15.geo. 也有C++(t15.cpp), Python(t15.py), Julia(t15.jl)和Fortran(t15.f90)版本.
// Gmsh GEO教程15
//
// 嵌入的点, 线和面
//
// 在默认情况下, Gmsh中跨几何维度的网格只有当低维实体位于高维实体的边界上时(即点, 曲线或面是体积的边界的一部分时)才是共形的.
// 嵌入约束允许强制网格与其他低维实体共形.
// 我们再次从包含第一个教程开始:
Include "t1.geo";
// 我们修改网格尺寸以生成更粗的网格
lc = lc * 4;
MeshSize {1:4} = lc;
// 我们定义一个新点
Point(5) = {0.02, 0.02, 0, lc};
// 可以使用" Point In Surface" 命令强制该点被" 嵌入" 到二维网格中:
Point{5} In Surface{1};
// 同样, 可以使用" Curve in Surface" 命令强制一条曲线嵌入到二维网格中:
Point(6) = {0.02, 0.12, 0, lc};
Point(7) = {0.04, 0.18, 0, lc};
Line(5) = {6, 7};
Curve{5} In Surface{1};
// 也可以使用" Curve/Point In Volume" 命令将点和曲线嵌入到体积中:
Extrude {0, 0, 0.1}{ Surface {1}; }
p = newp;
Point(p) = {0.07, 0.15, 0.025, lc};
Point{p} In Volume {1};
l = newc;
Point(p+1) = {0.025, 0.15, 0.025, lc};
Line(l) = {7, p+1};
Curve{l} In Volume {1};
// 最后, 还可以使用" Surface In Volume" 命令将一个面嵌入到体积中:
Point(p+2) = {0.02, 0.12, 0.05, lc};
Point(p+3) = {0.04, 0.12, 0.05, lc};
Point(p+4) = {0.04, 0.18, 0.05, lc};
Point(p+5) = {0.02, 0.18, 0.05, lc};
Line(l+1) = {p+2, p+3};
Line(l+2) = {p+3, p+4};
Line(l+3) = {p+4, p+5};
Line(l+4) = {p+5, p+2};
ll = newcl;
Curve Loop(ll) = {l+1:l+4};
s = news;
Plane Surface(s) = {ll};
Surface{s} In Volume {1};
// 注意, 使用OpenCASCADE内核(参见t16.geo)时, 当对不同维度的实体应用" BooleanFragments" 命令时, 如有必要, 低维实体将自动嵌入到高维实体中.
Physical Point("Embedded point") = {p};
Physical Curve("Embdded curve") = {l};
Physical Surface("Embedded surface") = {s};
Physical Volume("Volume") = {1};
2.16. 2.16 t16: 构造实体几何, OpenCASCADE几何内核
参见t16.geo. 也有C++(t16.cpp), C(t16.c), Python(t16.py), Julia(t16.jl)和Fortran(t16.f90)版本.
// Gmsh GEO教程16
//
// 构造实体几何, OpenCASCADE几何内核
//
//
// 从版本3开始, Gmsh允许直接使用其他几何内核, 而不是以自底向上的方式使用Gmsh的内置几何内核构建模型. 这里我们使用OpenCASCADE内核:
SetFactory("OpenCASCADE");
// 我们使用构造实体几何来构建与t5.geo中相同的模型.
// 首先创建两个立方体:
Box(1) = {0,0,0, 1,1,1};
Box(2) = {0,0,0, 0.5,0.5,0.5};
// 应用布尔差运算创建" 立方体减去八分之一" 的形状:
BooleanDifference(3) = { Volume{1}; Delete; }{ Volume{2}; Delete; };
// OpenCASCADE的布尔运算总会创建新的实体. 在参数中添加" Delete" 可以自动删除原始实体.
// 然后创建五个球体:
x = 0 ; y = 0.75 ; z = 0 ; r = 0.09 ;
For t In {1:5}
x += 0.166 ;
z += 0.166 ;
Sphere(3 + t) = {x,y,z,r};
Physical Volume(t) = {3 + t};
EndFor
// 如果我们想要五个空孔, 我们会再次使用" BooleanDifference" . 但这里我们想要五个球形内含物, 其网格应与立方体的网格共形: 因此我们使用" BooleanFragments" , 它以共形方式对所有体积进行相交处理(不会创建重复的界面):
v() = BooleanFragments{ Volume{3}; Delete; }{ Volume{3 + 1 : 3 + 5}; Delete; };
// 当布尔运算导致实体发生简单修改, 并且如果使用" Delete" 删除原始实体, Gmsh会尝试为新实体分配相同的标签. (此行为由" Geometry.OCCBooleanPreserveNumbering" 选项控制. )
// 这里上面定义的" Physical Volume" 仍然有效, 因为五个球体(体积4, 5, 6, 7和8)会被碎片操作删除, 但会以相同的标签重新创建(尽管带有新的表面).
// 立方体的标签会改变, 因此我们需要通过程序来访问它:
Physical Volume(10) = v(0);
// 使用构造实体几何创建实体非常强大, 但在一些方面可能会带来实际问题, 例如为点设置网格尺寸或识别边界时.
// 要识别点或其他边界实体, 可以利用" PointfsOf" (更通用的" Boundary" 命令的特例)和" In BoundingBox" 命令.
lcar1 = .1;
lcar2 = .0005;
lcar3 = .055;
eps = 1e-3;
// 为所有体积的所有点分配网格尺寸:
MeshSize{ PointsOf{ Volume{:}; } } = lcar1;
// 覆盖五个球体的点的此约束:
MeshSize{ PointsOf{ Volume{3 + 1 : 3 + 5}; } } = lcar3;
// 通过几何搜索选择角点:
p() = Point In BoundingBox{0.5-eps, 0.5-eps, 0.5-eps, 0.5+eps, 0.5+eps, 0.5+eps};
MeshSize{ p() } = lcar2;
// 使用OpenCASCADE几何内核创建的其他示例可在" t18.geo" , " t19.geo" 和" t20.geo" 中找到, 也可在" examples/boolean" 目录中找到.
2.17. 2.17 t17: 各向异性背景网格
参见t17.geo. 也有C++(t17.cpp), Python(t17.py), Julia(t17.jl)和Fortran(t17.f90)版本.
// Gmsh GEO教程17
// 各向异性背景网格
//
// 如t7.geo中所示, 通过提供背景网格(即包含目标网格尺寸的后处理视图)可以非常精确地指定网格尺寸.
// 这里, 背景网格表示为定义在正方形上的度量张量场. 在二维中, 应使用bamg作为二维网格生成器以启用各向异性网格.
SetFactory("OpenCASCADE");
// 创建一个正方形
Rectangle(1) = {-2, -2, 0, 4, 4};
// 合并包含目标各向异性网格尺寸的后处理视图
Merge "t17_bgmesh.pos";
// 将该视图应用为当前背景网格
Background Mesh View[0];
// 使用bamg
Mesh.SmoothRatio = 3;
Mesh.AnisoMax = 1000;
Mesh.Algorithm = 7;
2.18. 2.18 t18: 周期性网格
参见t18.geo. 也有C++(t18.cpp), Python(t18.py), Julia(t18.jl)和Fortran(t18.f90)版本.
// Gmsh GEO教程18
//
// 周期性网格
//
//
// 周期性网格约束可以施加在表面和曲线上.
// 让我们使用OpenCASCADE几何内核构建两个几何.
SetFactory("OpenCASCADE");
// 第一个几何非常简单: 一个单位立方体, 带有非均匀网格尺寸约束(故意设置以直观验证周期性约束是否有效):
Box(1) = {0, 0, 0, 1, 1, 1};
MeshSize {:} = 0.1;
MeshSize {1} = 0.02;
// 为了强制立方体表面2(右侧)的网格与表面1(左侧)的网格匹配, 设置以下周期性约束:
Periodic Surface {2} = {1} Translate {1, 0, 0};
// 在网格生成期间, 表面2上的网格将通过复制表面1上的网格来创建. 周期性约束可以通过" 平移" , " 旋转" 或一般" 仿射" 变换来指定.
// 可以以相同方式施加多个周期性约束:
Periodic Surface {6} = {5} Translate {0, 0, 1};
Periodic Surface {4} = {3} Translate {0, 1, 0};
// 对于更复杂的情况, 手动找到对应的表面可能很繁琐, 特别是当几何通过实体建模创建时. 让我们构建一个稍微复杂一些的几何.
// 我们从一个立方体和一些球体开始:
Box(10) = {2, 0, 0, 1, 1, 1};
x = 2-0.3; y = 0; z = 0;
Sphere(11) = {x, y, z, 0.35};
Sphere(12) = {x+1, y, z, 0.35};
Sphere(13) = {x, y+1, z, 0.35};
Sphere(14) = {x, y, z+1, 0.35};
Sphere(15) = {x+1, y+1, z, 0.35};
Sphere(16) = {x, y+1, z+1, 0.35};
Sphere(17) = {x+1, y, z+1, 0.35};
Sphere(18) = {x+1, y+1, z+1, 0.35};
// 首先对所有体积进行碎片操作, 这会使球体的部分突出到立方体外部:
v() = BooleanFragments { Volume{10}; Delete; }{ Volume{11:18}; Delete; };
// 要求OpenCASCADE使用STL网格计算实体更精确的边界框:
Geometry.OCCBoundsUseStl = 1;
// 然后检索原始立方体内边界框中的所有体积, 并删除外部的所有部分:
eps = 1e-3;
vin() = Volume In BoundingBox {2-eps,-eps,-eps, 2+1+eps,1+eps,1+eps};
v() -= vin();
Recursive Delete{ Volume{v()}; }
// 我们现在设置非均匀网格尺寸约束(再次为了直观检查结果):
MeshSize { PointsOf{ Volume{vin()}; }} = 0.1;
p() = Point In BoundingBox{2-eps, -eps, -eps, 2+eps, eps, eps};
MeshSize {p()} = 0.001;
// 我们现在自动识别几何左侧和右侧的对应表面.
// 首先获取左侧的所有表面:
Sxmin() = Surface In BoundingBox{2-eps, -eps, -eps, 2+eps, 1+eps, 1+eps};
For i In {0:#Sxmin()-1}
// 然后获取每个左侧表面的边界框
bb() = BoundingBox Surface { Sxmin(i) };
// 将边界框平移到右侧, 并查找其中的表面:
Sxmax() = Surface In BoundingBox { bb(0)-eps+1, bb(1)-eps, bb(2)-eps, bb(3)+eps+1, bb(4)+eps, bb(5)+eps };
// 对于所有匹配项, 比较相应的边界框...
For j In {0:#Sxmax()-1}
bb2() = BoundingBox Surface { Sxmax(j) };
bb2(0) -= 1;
bb2(3) -= 1;
// ...如果匹配, 则应用周期性约束
If(Fabs(bb2(0)-bb(0)) < eps && Fabs(bb2(1)-bb(1)) < eps &&
Fabs(bb2(2)-bb(2)) < eps && Fabs(bb2(3)-bb(3)) < eps &&
Fabs(bb2(4)-bb(4)) < eps && Fabs(bb2(5)-bb(5)) < eps)
Periodic Surface {Sxmax(j)} = {Sxmin(i)} Translate {1,0,0};
EndIf
EndFor
EndFor
2.19. 2.19 t19: 截面体, 倒圆角, 管道, 基于曲率的网格尺寸
参见t19.geo. 也有C++(t19.cpp), Python(t19.py), Julia(t19.jl)和Fortran(t19.f90)版本.
// Gmsh GEO教程19
//
// 截面体, 倒圆角, 管道, 基于曲率的网格尺寸
//
//
// OpenCASCADE几何内核支持实体建模的几个有用功能.
SetFactory("OpenCASCADE");
// 可以通过(闭合)曲线环使用" ThruSections" 命令构造体积
Circle(1) = {0,0,0, 0.5};
Circle(2) = {0.1,0.05,1, 0.1};
Circle(3) = {-0.1,-0.1,2, 0.3};
Curve Loop(1) = 1;
Curve Loop(2) = 2;
Curve Loop(3) = 3;
ThruSections(1) = {1:3};
// 使用" Ruled ThruSections" 可以强制使用直纹面:
Circle(11) = {2+0,0,0, 0.5};
Circle(12) = {2+0.1,0.05,1, 0.1};
Curve Loop(11) = 11;
Curve Loop(12) = 12;
Circle(13) = {2-0.1,-0.1,2, 0.3};
Curve Loop(13) = 13;
Ruled ThruSections(11) = {11:13};
// 复制第一个体积, 并对其所有边进行倒圆角:
v() = Translate{4, 0, 0} { Duplicata{ Volume{1}; } };
f() = Abs(Boundary{ Volume{v(0)}; });
e() = Unique(Abs(Boundary{ Surface{f()}; }));
Fillet{v(0)}{e()}{0.1}
// OpenCASCADE还允许沿平滑路径进行一般拉伸. 让我们首先定义一条样条曲线:
nturns = 1;
npts = 20;
r = 1;
h = 1 * nturns;
For i In {0 : npts - 1}
theta = i * 2*Pi*nturns/npts;
Point(1000 + i) = {r * Cos(theta), r * Sin(theta), i * h/npts};
EndFor
Spline(1000) = {1000 : 1000 + npts - 1};
// 线框类似于曲线环, 但为开放的:
Wire(1000) = {1000};
// 我们定义想要沿样条拉伸的形状(一个圆盘):
Disk(1000) = {1,0,0, 0.2};
Rotate {{1, 0, 0}, {0, 0, 0}, Pi/2} { Surface{1000}; }
// 我们沿样条拉伸圆盘以创建管道:
Extrude { Surface{1000}; } Using Wire {1000}
// 我们删除源表面, 并增加子边的数量以更好地显示几何:
Delete{ Surface{1000}; }
Geometry.NumSubEdges = 1000;
// 我们可以激活基于曲率的网格单元尺寸计算(这里目标是每2*Pi弧度有20个单元):
Mesh.MeshSizeFromCurvature = 20;
// 我们可以约束最小和最大单元尺寸以保持在合理范围内(更多细节参见t10.geo):
Mesh.MeshSizeMin = 0.001;
Mesh.MeshSizeMax = 0.3;
2.20. 2.20 t20: STEP导入与操作, 几何分区
参见t20.geo. 也有C++(t20.cpp), Python(t20.py), Julia(t20.jl)和Fortran(t20.f90)版本.
//
// Gmsh GEO教程20
//
// STEP导入与操作, 几何分区
//
//
// OpenCASCADE几何内核允许导入STEP文件并对其进行修改. 在本教程中, 我们将加载一个STEP几何并将其分区为多个切片.
SetFactory("OpenCASCADE");
// 加载一个STEP文件(使用" ShapeFromFile" 而不是" Merge" 可以直接获取导入的最高维度实体的标签):
v() = ShapeFromFile("t20_data.step");
// 如果我们在合并STEP文件之前指定
//
// Geometry.OCCTargetUnit = "M";
//
// OpenCASCADE会将单位转换为米(而不是默认的毫米).
// 获取体积的边界框:
bbox() = BoundingBox Volume{v()};
xmin = bbox(0);
ymin = bbox(1);
zmin = bbox(2);
xmax = bbox(3);
ymax = bbox(4);
zmax = bbox(5);
// 我们想要将模型切成N个切片, 要么保留体积切片, 要么只保留切割得到的表面:
DefineConstant[
N = {5, Min 2, Max 100, Step 1, Name "Parameters/0切片数量"}
dir = {0, Choices{0="X", 1="Y", 2="Z"}, Name "Parameters/1方向"}
surf = {0, Choices{0, 1}, Name "Parameters/2仅保留表面? "}
];
dx = (xmax - xmin);
dy = (ymax - ymin);
dz = (zmax - zmin);
L = (dir == 0) ? dz : dx;
H = (dir == 1) ? dz : dy;
// 创建第一个切割平面:
s() = {news};
If(dir == 0)
Rectangle(s(0)) = {xmin, ymin, zmin, L, H};
ElseIf(dir == 1)
Rotate{ {0, 1, 0}, {xmin, ymin, zmin}, -Pi/2 } { Surface{s(0)}; }
Else
Rotate{ {1, 0, 0}, {xmin, ymin, zmin}, Pi/2 } { Surface{s(0)}; }
EndIf
tx = (dir == 0) ? dx / N : 0;
ty = (dir == 1) ? dy / N : 0;
tz = (dir == 2) ? dz / N : 0;
Translate{tx, ty, tz} { Surface{s(0)}; }
// 创建其他切割平面:
For i In {1:N-2}
s() += Translate{i * tx, i * ty, i * tz} { Duplicata{ Surface{s(0)}; } };
EndFor
// 将体积与所有切割平面进行碎片操作(即相交):
BooleanFragments{ Volume{v()}; Delete; }{ Surface{s()}; Delete; }
// 现在删除所有不在体积边界上的表面(及其边界实体), 即" 突出" 到体积外部的切割平面部分:
Recursive Delete { Surface{:}; }
If(surf)
// 如果我们只想保留表面, 在切割平面周围的边界框中检索表面...
eps = 1e-4;
s() = {};
For i In {1:N-1}
xx = (dir == 0) ? xmin : xmax;
yy = (dir == 1) ? ymin : ymax;
zz = (dir == 2) ? zmin : zmax;
s() += Surface In BoundingBox
{xmin - eps + i * tx, ymin - eps + i * ty, zmin - eps + i * tz,
xx + eps + i * tx, yy + eps + i * ty, zz + eps + i * tz};
EndFor
// ...并删除所有其他实体:
dels = Surface{:};
dels -= s();
Delete { Volume{:}; Surface{dels()}; Curve{:}; Point{:}; }
EndIf
// 最后, 指定全局网格尺寸:
Mesh.MeshSizeMin = 3;
Mesh.MeshSizeMax = 3;
// 要对网格而不是几何进行分区, 参见t21.geo.
3. 第3章: Gmsh图形用户界面
一旦安装好Gmsh应用程序(参见1.7节[在计算机上安装和运行Gmsh], 第14页), 要启动图形界面, 只需双击Gmsh图标, 或在终端的命令提示符下输入命令. 这将打开Gmsh图形用户界面的主窗口, 顶部有一个菜单栏(在macOS上, 默认情况下菜单栏在屏幕顶部-–—可以通过" General.SystemMenuBar" 选项更改, 参见7.1节[通用选项], 第225页), 左侧有一个树形菜单(默认包含一个" Modules" 条目, 其下有三个子项: " Geometry" , " Mesh" 和" Solver" ), 右侧是图形区域, 底部有一个带有一些快捷按钮的状态栏. (可以使用" Window>Attach/Detach Menu" 分离树形菜单. )
要创建新的几何模型, 使用" File->New" 菜单创建一个新的模型文件, 例如选择" mymodel.geo" 作为文件名. 然后在树形菜单中, 依次打开" Geometry" , " Elementary entities" 和" Add" 子菜单, 例如点击" Rectangle" . 会弹出一个带有参数的上下文窗口: 可以在这个窗口中输入一些参数(例如矩形的宽度和高度), 然后移动鼠标将其放置在画布上. 如果不想用鼠标放置矩形, 在窗口中选择" X" , " Y" 和" Z freeze" , 并在上下文窗口中手动输入坐标. 完成后, 按" e" (参见图形窗口顶部的状态消息)或点击上下文窗口中的" Add" 按钮.
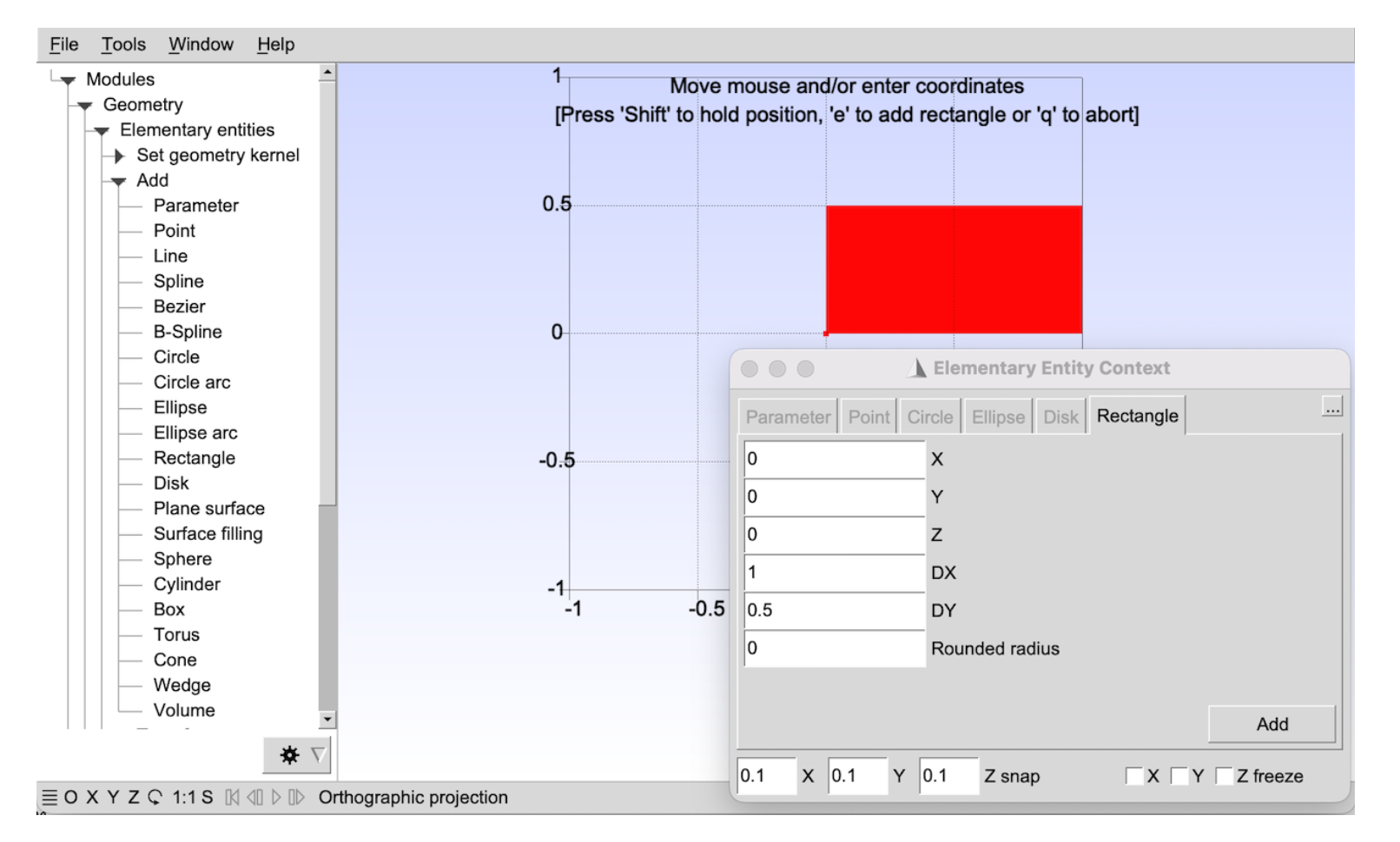
无需保存几何模型: 添加矩形时, 脚本命令会自动附加到模型文件"mymodel.geo" 中:
//+
SetFactory("OpenCASCADE");
Rectangle(1) = {0, 0, 0, 1, 0.5, 0};
可以用任何文本编辑器编辑此脚本; 点击树形菜单中的" Edit script" 将启动" General.Editor" 选项指定的默认文本编辑器(参见7.1节[通用选项], 第225页). 如果编辑了脚本, 应点击树形菜单中的" Reload script" 在图形界面中重新加载修改内容. 脚本中的//+行是一个注释, 用作图形界面添加的命令之间的标记; 参见第5章[Gmsh脚本语言], 第91页获取脚本语言参考.
结合图形界面操作和脚本文件编辑是使用Gmsh应用程序的经典方式. 例如, 直接在脚本文件中定义变量和点通常更快, 然后使用图形界面交互式地定义曲线, 曲面和体积.
要加载现有模型而不是从头创建模型, 使用" File->Open" 菜单. 例如, 要打开第一个教程(参见第2章[Gmsh教程], 第15页), 选择t1.geo. 在终端上, 也可以在命令行中直接指定文件名, 即:
> gmsh t1.geo
要生成网格, 在树形菜单中打开" Mesh" 并选择所需的维度: " 1D" 将网格化所有曲线; " 2D" 将网格化所有曲面-–—如果之前未调用" 1D" , 也会网格化所有曲线; " 3D" 将网格化所有体积-–—如果之前未调用" 2D" , 也会网格化所有曲面. 要以当前网格格式保存生成的网格, 点击树形菜单中的" Save" , 或使用" File->Export" 菜单选择适当的格式和文件名. 默认的网格文件名基于当前活动模型的名称, 附加的扩展名取决于网格格式. 注意, 大多数交互式命令都有键盘快捷键: 参见3.2节[键盘快捷键], 第82页, 或在菜单中选择" Help->Keyboard and Mouse Usage". 例如, 要快速生成2D网格并保存, 可先按2, 再按Ctrl+Shift+s.
在图形窗口中双击将弹出一个快速快捷菜单, 可用于例如快速切换网格实体(如曲面面)的可见性, 重置视口, 选择旋转中心, 显示轴, 或访问完整的模块选项(从" Tools->Options" 菜单). 状态栏左下角的快捷按钮可用于快速调整视口: " X" , " Y" , " Z" 设置视口, 使相应的轴垂直于图形平面; 旋转按钮将视图旋转90度; " 1:1" 重置缩放比例.
可以同时加载多个文件. 在命令行中指定时, 第一个文件定义活动模型(与使用" File->Open" 菜单相同), 其他文件" 合并" 到该模型中(与使用" File->Merge" 菜单相同). 例如, 要将文件view1.pos和view5.msh中包含的后处理视图与第一个教程(2.1节[t1], 第15页)的几何图形合并, 可以输入以下命令:
> gmsh t1.geo view1.pos view5.msh
当加载一个或多个后处理视图时, 树形菜单中会出现" Post-Processing" 条目. 通过前面的命令, 树形菜单的" Post-processing" 下会出现三个视图, 分别标记为" A scalar map" , " Nodal scalar map" 和" Element 1 vector" . 在这个例子中, 视图包含多个时间步: 可以使用状态栏左侧的快捷图标循环浏览. 点击视图名称将切换所选视图的可见性, 点击右侧的箭头按钮可访问视图的选项.
注意, 所有交互式指定的选项也可以直接在脚本文件中指定. 可以使用" File->Save Model Options" 保存当前活动模型的当前选项. 这将创建一个新的选项文件, 文件名与活动模型相同, 但添加了额外的" .opt" 扩展名. 下次打开此模型时, 相关选项也会自动加载. 要将当前选项保存为所有未来Gmsh会话的默认偏好设置, 改用" File->Save Options As Default" 菜单. 也可以通过在" File->Export" 中选择" Gmsh options" 格式, 将当前选项保存到任意文件中. 有关可用选项的更多信息(以及如何将其重置为默认值), 参见第7章[Gmsh选项], 第225页. 也可以使用" Help->Current Options" 菜单获取所有选项及其当前值的完整列表.
最后, 注意图形界面也可以使用API运行(和修改): 参见6.15节[gmsh/fltk命名空间], 第215页了解详情.
接下来的两节描述图形界面中的鼠标操作以及所有预定义的键盘快捷键. 解释如何使用Gmsh图形界面的屏幕录像可在以下地址在线获取: https://gmsh.info/screencasts/.
3.1. 3.1 鼠标操作
- 移动: 高亮显示鼠标指针下的实体并显示其属性 / 调整套索缩放或套索(取消)选择的大小
- 左键: 旋转 / 选择实体 / 确认套索缩放或套索选择 - Ctrl+左键: 开始套索缩放或套索(取消)选择
- 中键: 缩放 / 取消选择实体 / 确认套索缩放或套索取消选择 - Ctrl+中键: 正交化显示
- 右键: 平移 / 取消套索缩放或套索(取消)选择 / 在post-processing视图按钮上弹出菜单
- Ctrl+右键: 重置为默认视点
对于两键鼠标, 中键=Shift+左键.
对于单键鼠标, 中键=Shift+左键, 右键=Alt+左键.
3.2. 3.2 键盘快捷键
(在macOS上, 以下快捷键中的Ctrl替换为Cmd. )
| 快捷键 | 功能 |
|---|---|
| 左箭头 | 前往上一个时间步 |
| 右箭头 | 前往下一个时间步 |
| 上箭头 | 显示上一个视图 |
| 下箭头 | 显示下一个视图 |
| 0 | 重新加载几何图形 |
| Ctrl+0或9 | 重新加载整个项目 |
| 1或F1 | 网格线 |
| 2或F2 | 网格面 |
| 3或F3 | 网格体 |
| Escape | 取消套索缩放/选择, 切换鼠标选择开关 |
| e | 在几何创建模式中结束/确认选择 |
| g | 进入几何模块 |
| m | 进入网格模块 |
| p | 进入后处理模块 |
| q | 在几何创建模式中中止选择 |
| s | 进入求解器模块 |
| x | 在几何创建模式中切换x坐标锁定 |
| y | 在几何创建模式中切换y坐标锁定 |
| z | 在几何创建模式中切换z坐标锁定 |
| Shift+a | 将所有窗口置于前端 |
| Shift+g | 显示几何选项 |
| Shift+m | 显示网格选项 |
| Shift+o | 显示通用选项 |
| Shift+p | 显示后处理选项 |
| Shift+s | 显示求解器选项 |
| Shift+u | 显示后处理视图插件 |
| Shift+w | 显示后处理视图选项 |
| Shift+x | 在几何创建模式中仅沿x坐标移动 |
| Shift+y | 在几何创建模式中仅沿y坐标移动 |
| Shift+z | 在几何创建模式中仅沿z坐标移动 |
| Shift+Escape | 启用完全鼠标选择 |
| 快捷键 | 功能 |
|---|---|
| Ctrl+d | 附加/分离菜单 |
| Ctrl+e | 导出项目 |
| Ctrl+f | 进入全屏 |
| Ctrl+i | 显示统计窗口 |
| Ctrl+j | 保存模型选项 |
| Ctrl+l | 显示消息控制台 |
| Ctrl+m | 最小化窗口 |
| Ctrl+n | 创建新的项目文件 |
| Ctrl+o | 打开项目文件 |
| Ctrl+q | 退出 |
| Ctrl+r | 重命名项目文件 |
| Ctrl+s | 以默认格式保存网格 |
| Shift+Ctrl+c | 显示裁剪平面窗口 |
| Shift+Ctrl+h | 显示当前选项和工作区窗口 |
| Shift+Ctrl+j | 将选项保存为默认值 |
| Shift+Ctrl+m | 显示操纵器窗口 |
| Shift+Ctrl+n | 显示选项窗口 |
| Shift+Ctrl+o | 合并文件 |
| Shift+Ctrl+r | 打开倒数第二个打开的文件 |
| Shift+Ctrl+u | 显示插件窗口 |
| Shift+Ctrl+v | 显示可见性窗口 |
| Alt+a | 循环轴模式 |
| Alt+b | 隐藏/显示边界框 |
| Alt+c | 循环预定义配色方案 |
| Alt+e | 隐藏/显示可见后处理视图的元素轮廓 |
| Alt+f | 更改重绘模式(快速/完整) |
| Alt+h | 隐藏/显示所有后处理视图 |
| Alt+i | 隐藏/显示所有后处理视图比例尺 |
| Alt+l | 隐藏/显示几何线 |
| Alt+m | 切换所有网格实体的可见性 |
| 快捷键 | 功能 |
|---|---|
| Alt+n | 隐藏/显示所有后处理视图注释 |
| Alt+o | 更改投影模式(正交/透视) |
| Alt+p | 隐藏/显示几何点 |
| Alt+r | 循环可见后处理视图的范围模式 |
| Alt+s | 隐藏/显示几何面 |
| Alt+t | 循环可见后处理视图的间隔模式 |
| Alt+v | 隐藏/显示几何体 |
| Alt+w | 启用/禁用所有照明 |
| Alt+x | 设置X视图 |
| Alt+y | 设置Y视图 |
| Alt+z | 设置Z视图 |
| Alt+1 | 设置1:1视图 |
| Alt+Shift+a | 隐藏/显示小轴 |
| Alt+Shift+b | 隐藏/显示网格体表面 |
| Alt+Shift+c | 循环预定义颜色映射 |
| Alt+Shift+d | 隐藏/显示网格面表面 |
| Alt+Shift+l | 隐藏/显示网格线 |
| Alt+Shift+p | 隐藏/显示网格节点 |
| Alt+Shift+s | 隐藏/显示网格面边缘 |
| Alt+Shift+t | 与Alt+t相同, 但包含数字模式 |
| Alt+Shift+v | 隐藏/显示网格体边缘 |
| Alt+Shift+x | 设置-X视图 |
| Alt+Shift+y | 设置-Y视图 |
| Alt+Shift+z | 设置-Z视图 |
| Alt+Shift+1 | 围绕可见实体重置边界框 |
| Alt+Ctrl+1 | 同步视口之间的缩放 |
4. 第4章: Gmsh命令行界面
Gmsh定义了许多命令行开关, 可用于从命令行以" 批处理" 模式控制Gmsh, 无需借助脚本(参见第5章[Gmsh脚本语言], 第91页)或API(参见第6章[Gmsh应用程序编程接口], 第125页)即可传递选项.
例如, 在批处理模式下对第一个教程进行网格划分, 可在终端中使用-2命令行开关:
> gmsh t1.geo -2
通过在' t1.geo'末尾添加 Mesh 2; 命令并运行
> gmsh t1.geo -parse_and_exit
或者进一步在脚本末尾添加 Exit; 命令, 然后直接打开这个新文件, 也能达到同样的效果:
> gmsh t1.geo
请注意, 所有数值和字符串选项(参见第7章[Gmsh选项], 第225页)都可以通过命令行中的 -setnumber 和 -setstring 开关进行设置
> gmsh t1.geo -setnumber Mesh.Nodes 1 -setnumber Geometry.SurfaceLabels 1
下面给出所有命令行开关的列表.
(相关的选项名称如有, 将放在括号中)
几何相关:
- -0: 输出模型, 然后退出
- -tol value: 设置几何公差(Geometry.Tolerance) - -match: 匹配几何和网格
网格相关:
- -1, -2, -3: 执行1D, 2D或3D网格生成, 然后退出
- -format string: 选择输出网格格式: auto, msh1, msh2, msh22, msh3, msh4, msh40, msh41, msh, unv, vtk, wrl, mail, stl, p3d, mesh, bdf, cgns, med, diff, ir3, inp, ply2, celum, su2, x3d, dat, neu, m, key, off, rad, obj(Mesh.Format) -
-bin: 尽可能创建二进制文件(Mesh.Binary) - -refine: 执行均匀网格细化, 然后退出 - -barycentricrefine: 执行重心网格细化, 然后退出 - -reclassify angle: 重新分类表面网格, 然后退出 - -reparam angle: 重新参数化表面网格, 然后退出 - -hybrid: 生成混合六面体-四面体网格, 过渡处使用三棱柱 - -part int: 批处理网格生成后进行分区(Mesh.NbPartitions) - -partweight [tri,quad,tet,hex,pri,pyr,trih] int: 分区时三角形/四边形等的权重(Mesh.Partition[Tri,Quad,…]Weight) - -partsplit: 将网格分区保存到单独的文件中(Mesh.PartitionSplitMeshFiles) - -part_[no_]topo: 创建分区拓扑(Mesh.PartitionCreateTopology) - -part_[no_]ghosts: 创建幽灵单元(Mesh.PartitionCreateGhostCells) - -part_[no_]physicals: 为分区创建物理组(Mesh.PartitionCreatePhysicals) - -parttopopro: 保存分区拓扑.pro文件(Mesh.PartitionTopologyFile) - -preservenumberingmsh2: 在MSH2格式中保留单元编号(Mesh.PreserveNumberingMsh2) - -saveall: 保存所有单元(Mesh.SaveAll) - -saveparametric: 保存带有参数坐标的节点(Mesh.SaveParametric) - -savetopology: 保存模型拓扑(Mesh.SaveTopology) - -algo string: 选择网格算法: auto, meshadapt, del2d, front2d, delquad, quadqs, initial2d, del3d, front3d, mmg3d, hxt, initial3d(Mesh.Algorithm和Mesh.Algorithm3D) - -smooth int: 设置网格平滑步骤数(Mesh.Smoothing) - -order int: 设置网格阶数(Mesh.ElementOrder) - -optimize[netgen]: 优化四面体单元质量(Mesh.Optimize[Netgen]) - -optimizethreshold: 优化质量低于阈值的四面体单元(Mesh.OptimizeThreshold) - -optimizeho: 优化高阶网格(Mesh.HighOrderOptimize) - -ho_[min,max,nlayers]: 高阶优化参数(Mesh.HighOrderThreshold[Min,Max], Mesh.HighOrderNumLayers) - -clscale value: 设置网格单元大小因子(Mesh.MeshSizeFactor) - -clmin value: 设置最小网格单元大小(Mesh.MeshSizeMin) - -clmax value: 设置最大网格单元大小(Mesh.MeshSizeMax) - -clextend value: 从边界扩展网格单元大小(Mesh.MeshSizeExtendFromBoundary) - -clcurv value: 根据曲率计算网格单元大小, 该值为每2π弧度的目标单元数(Mesh.MeshSizeFromCurvature) - -anisomax value: 设置bamg的最大各向异性(Mesh.AnisoMax) - -smoothratio value: 设置bamg在节点间的网格大小平滑比率(Mesh.SmoothRatio) - -epslc1d value: 设置1D网格的网格大小场评估精度(Mesh.LcIntegrationPrecision) - -swapangle value: 设置相邻两个面之间允许交换的阈值角度(度)(Mesh.AllowSwapAngle) - -rand value: 设置随机扰动因子(Mesh.RandomFactor) - -bgm file: 从文件加载背景网格 - -check: 对网格执行各种一致性检查 - -ignoreperiocity: 忽略周期性边界(Mesh.IgnorePeriodicity)
后处理相关: - -link int: 选择视图之间的链接模式(PostProcessing.Link) - -combine: 将名称相同的视图合并为多时间步视图
求解器相关: - -listen string: 始终监听传入的连接请求(Solver.AlwaysListen)到指定的套接字(如果未指定, 则使用Solver.SocketName) - -minterpreter string: Octave解释器的名称(Solver.OctaveInterpreter) - -pyinterpreter string: Python解释器的名称(Solver.OctaveInterpreter) - -run: 运行ONELAB求解器
显示相关: - -n: 启动时隐藏所有网格和后处理视图(View.Visible, Mesh.[Points,Lines,SurfaceEdges,…]) - -nodb: 禁用双缓冲(General.DoubleBuffer) - -numsubedges: 设置高阶单元显示的细分数量(Mesh.NumSubEdges) - -fontsize int: 指定GUI的字体大小(General.FontSize) - -theme string: 指定FLTK GUI主题(General.FltkTheme) - -display string: 指定显示器(General.Display) - -camera: 使用相机模式视图(General.CameraMode) - -stereo: OpenGL四缓冲立体渲染(General.Stereo) - -gamepad: 如果可用, 使用游戏手柄控制器
其他: - -, -parseandexit: 解析输入文件, 然后退出 - -save: 保存输出文件, 然后退出 - -o file: 指定输出文件名 - -new: 合并下一个文件之前创建新模型 - -merge: 合并下一个文件 - -open: 打开下一个文件 - -log filename: 将所有消息记录到filename - -a, -g, -m, -s, -p: 以自动, 几何, 网格, 求解器或后处理模式启动(General.InitialModule) - -pid: 在标准输出上打印进程ID - -watch pattern: 当符合pattern的文件可用时合并它们(General.WatchFilePattern) - -bg file: 加载背景(图像或PDF)文件(General.BackgroundImageFileName) - -v int: 设置详细程度级别(General.Verbosity) - -string "string": 在启动时解析命令字符串 - -setnumber name value: 设置常量, ONELAB或选项数值name=value - -setstring name value: 设置常量, ONELAB或选项字符串name=value - -nopopup: 在脚本中不弹出对话框窗口(General.NoPopup) - -noenv: 启动时不修改环境 - -nolocale: 启动时不修改区域设置 - -option file: 在启动时解析选项文件 - -convert files: 将文件转换为最新的二进制格式, 然后退出 - -nt int: 设置线程数(General.NumThreads) - -cpu: 报告所有操作的CPU时间 - -version: 显示版本号 - -info: 显示详细的版本信息 - -help: 显示命令行使用方法 - -helpoptions: 显示所有选项
5. 第五章: Gmsh脚本语言
Gmsh脚本语言由Gmsh的解析器在运行时解释执行. 脚本写在ASCII文件中, 通常以" .geo" 为扩展名, 但也可以使用其他扩展名(或无扩展名). 例如, Gmsh经常使用" .pos" 扩展名为包含后处理命令的脚本, 特别是解析后的后处理视图(参见5.4节[后处理脚本命令], 第119页).
从历史上看, " .geo" 脚本一直是使用Gmsh执行复杂任务的主要方式, 它们确实非常强大: 可以处理浮点型(参见5.1.2节[浮点表达式], 第91页)和字符串型(参见5.1.3节[字符串表达式], 第94页)变量(没有整数类型), 循环和条件判断(参见5.1.8节[循环和条件语句], 第98页), 宏(参见5.1.7节[用户定义宏], 第98页)等. 然而, 与实际编程语言相比, Gmsh的脚本语言仍然相当有限: 例如, 没有私有变量, 宏不接受参数, 解析器的运行时解释可能会影响大型模型的性能. 因此, 根据工作流程和应用场景, 使用Gmsh API(参见第6章[Gmsh应用程序编程接口], 第125页)有时可能更合适. API的缺点是, 虽然脚本语言内置在Gmsh中, 因此可以直接在独立的Gmsh应用程序中使用, 但API需要外部依赖(C++, C或Fortran编译器; 或Python或Julia解释器).
本章通过先详细介绍通用命令(参见5.1节[通用脚本命令], 第91页), 再详细介绍几何(参见5.2节[几何脚本命令], 第104页), 网格(参见5.3节[网格脚本命令], 第113页)和后处理(参见5.4节[后处理脚本命令], 第119页)模块特有的脚本命令, 来描述脚本语言.
在本章其余部分描述脚本语言时, 使用以下规则(请注意, 元语法变量定义在整章中有效, 不仅在定义它们的部分中有效): 1. 关键字和文字符号如下所示. 2. 元语法变量(即不是语法一部分, 而是代表其他文本部分的文本片段)如下所示. 3. 元语法变量后的冒号(:)将变量与其定义分开. 4. 可选规则用<>对括起来. 5. 多个选择用|分隔. 6. 三个点(…)表示前面的规则可能(多次)重复.
5.1. 5.1 通用脚本命令
5.1.1. 5.1.1 注释
Gmsh脚本文件支持C和C++风格的注释: 1. 位于//和//对之间的任何文本都被忽略; 2. 双斜杠//之后的行的其余部分被忽略.
这些命令在双引号内或关键字内不会产生所述效果. 另请注意, 所有表达式中的" 空白字符" (空格, 制表符, 换行符)都被忽略.
5.1.2. 5.1.2 浮点表达式
Gmsh脚本中使用的两种常量类型是实数和字符串(没有整数类型). 这些类型的含义和语法与C或C++编程语言中的相同. 浮点表达式(或更简单地说, " 表达式" )由元语法变量=expression=表示, 在解析脚本文件时进行求值:
expression: real |
string | string ~ { expression } string [ expression ] |
# string [ ] |
( expression ) |
operator-unary-left expression |
expression operator-unary-right | expression operator-binary expression | expression operator-ternary-left expression built-in-function | operator-ternary-right expression |
number-option |
Find(expression-list-item, expression-list-item) | StrFind(string-expression, string-expression) | StrCmp(string-expression, string-expression) |
StrLen(string-expression) |
TextAttributes(string-expression<,string-expression...>) | Exists(string) | Exists(string~{ expression }) | FileExists(string-expression) |
StringToName(string-expression) | S2N(string-expression) | GetNumber(string-expression <,expression>) |
GetValue("string", expression) |
DefineNumber(expression, onelab-options)
此类表达式在大多数Gmsh脚本命令中使用. 当字符串=string=后附加~{expression}时, 结果是一个新字符串, 由=string=, _(下划线)和表达式的值连接而成. 这在循环中特别有用(参见5.1.8节[循环和条件语句], 第98页), 因为它允许自动定义唯一的字符串. 例如:
For i In {1:3}
EndFor x~{i} = i;
等同于
x_1 = 1; x_2 = 2; x_3 = 3;
方括号[]允许从列表中提取一个项(也可以使用圆括号代替方括号). #允许获取列表的大小. operator-unary-left, operator-unary-right, operator-binary, operator-ternary-left和operator-ternary-right运算符在5.1.5节[运算符](第95页)中定义. 关于内置函数的定义, 请参见5.1.6节[内置函数](第97页). 各种数字选项在第7章[Gmsh选项](第225页)中列出. Find在第二个表达式中搜索第一个表达式的出现(两者都可以是列表). StrFind在第一个字符串表达式中搜索第二个字符串表达式的任何出现. StrCmp比较两个字符串(根据第一个字符串大于, 等于或小于第二个字符串, 返回大于0, 等于0或小于0的整数). StrLen返回字符串的长度. TextAttributes创建文本字符串的属性. Exists检查具有给定名称的变量是否存在(即先前已定义), FileExists检查具有给定名称的文件是否存在. StringToName根据提供的字符串创建一个名称. GetNumber允许获取ONELAB变量的值(可选的第二个参数是变量不存在时返回的默认值). GetValue允许交互式地向用户请求一个值(第二个参数是非交互式模式下返回的值). 例如, 在输入文件中插入GetValue("参数alpha的值? ",5.76)将向用户查询某个参数alpha的值, 假设默认值为5.76. 如果设置了General.NoPopup选项(参见7.1节[通用选项], 第225页), 则不会询问, 而是自动使用默认值.
DefineNumber允许在一行中定义ONELAB变量. 作为第一个参数给出的表达式是默认值; 后面是各种ONELAB选项. 有关更多信息, 请参见ONELAB教程wiki.
表达式列表也被广泛使用, 其定义如下:
expression-list: expression-list-item <, expression-list-item> ...
with
expression-list-item: expression |
expression : expression | expression : expression : expression |
string [ ] | string ( ) | List [ string ] |
List [ expression-list-item ] |
List [ { expression-list } ] |
Unique [ expression-list-item ] |
Abs [ expression-list-item ] | ListFromFile [ expression-char ] |
LinSpace[ expression, expression, expression ] |
LogSpace[ expression, expression, expression ] |
string [ { expression-list } ] | Point { expression } |
transform |
boolean | extrude |
Point|Curve|Surface|Volume In BoundingBox { expression-list } | BoundingBox Point|Curve|Surface|Volume { expression-list } |
Mass Curve|Surface|Volume { expression } | CenterOfMass Curve|Surface|Volume { expression } | MatrixOfInertia Curve|Surface|Volume { expression } |
Point { expression } |
Physical Point|Curve|Surface|Volume { expression-list } | <Physical> Point|Curve|Surface|Volume { : } |
最后一个定义中的第二种情况允许创建包含两个表达式之间的数字范围的列表, 增量为1. 第三种情况也允许创建包含两个表达式之间的数字范围的列表, 但增量为等于第三个表达式的正数或负数. 第四, 五, 六种情况允许引用表达式列表(也可以使用圆括号代替方括号). Unique对列表中的条目进行排序并删除所有重复项. Abs取列表中所有条目的绝对值. ListFromFile从文件中读取数字列表. LinSpace和LogSpace使用线性或对数间隔构造列表. 接下来的两种情况允许引用表达式子列表(其元素是与表达式列表提供的索引对应的元素). 接下来的情况允许检索通过几何变换, 挤压和布尔运算创建的实体的索引(参见5.2.7节[变换], 第110页, 5.2.5节[挤压], 第108页和5.2.6节[布尔运算], 第109页).
允许在边界框中检索实体, 或获取给定实体的边界框, 边界框指定为(X最小值, Y最小值, Z最小值, X最大值, Y最大值, Z最大值). 请注意, 坐标的顺序与场景的BoundingBox命令中的不同: 参见5.1.2节[浮点表达式](第91页). 最后几种情况允许检索实体的质量, 质心或惯性矩阵, 给定几何点的坐标(参见5.2.1节[点], 第104页), 构成物理组的基本实体, 以及模型中所有(物理或基本)点, 曲线, 曲面或体积的标记. 这些操作都会触发CAD模型与内部Gmsh模型的同步.
要了解此类表达式的实际使用, 请查看第2章[Gmsh教程](第15页)中的前几个示例. 请注意, 为了简化语法, 如果表达式列表只包含一个项, 则可以省略包围表达式列表的大括号{}. 另请注意, 带括号的表达式列表前可以加一个减号, 以更改所有表达式列表项的符号.
对于某些命令, 可以在列表中指定所有可能的表达式. 这通过=expression-list-or-all=实现, 定义如下:
expression-list-or-all: expression-list | :
" all" (:)的含义取决于上下文. 例如, Curve{:}将获取模型中所有现有曲线的ID, 而Surface{:}将获取所有现有曲面的ID.
5.1.3. 5.1.3 字符串表达式
字符串表达式定义如下:
string-expression: "string" |
string | string[ expression ] | Today | OnelabAction | GmshExecutableName | CurrentDirectory | CurrentDir | CurrentFileName
StrPrefix ( string-expression ) |
StrRelative ( string-expression ) | StrCat ( string-expression <,...> ) | Str ( string-expression <,...> ) | StrChoice ( expression, string-expression, string-expression ) | StrSub( string-expression, expression, expression ) | StrSub( string-expression, expression ) | UpperCase ( string-expression ) | AbsolutePath ( string-expression ) |
DirName ( string-expression ) |
Sprintf ( string-expression , expression-list ) |
Sprintf ( string-expression ) | Sprintf ( string-option ) |
GetEnv ( string-expression ) | GetString ( string-expression <,string-expression>) | GetStringValue ( string-expression , string-expression ) | StrReplace ( string-expression , string-expression , string-expression )
NameToString ( string ) | N2S ( string ) |
<Physical> Point|Curve|Surface|Volume { expression } | DefineString(string-expression, onelab-options)
Today返回当前日期. OnelabAction返回当前的ONELAB动作(例如check或compute). GmshExecutableName返回Gmsh可执行文件的完整路径.
CurrentDirectory(或CurrentDir)和CurrentFileName返回正在解析的脚本的目录和文件名. StrPrefix和StrRelative获取给定文件名的前缀(例如, 去除扩展名)或相对路径. StrCat和Str连接字符串表达式(Str在除最后一个字符串外的每个字符串后添加一个换行符). StrChoice根据表达式的值返回第一个或第二个字符串表达式. StrSub返回字符串的一部分, 从第一个表达式给出的字符位置开始, 跨越第二个表达式给出的字符数或直到字符串末尾(以先到者为准; 如果未提供第二个表达式, 则始终到末尾). UpperCase将字符串表达式转换为大写. AbsolutePath返回文件的绝对路径. DirName返回文件的目录. Sprintf等同于C函数sprintf(其中string-expression是可以包含浮点格式字符的格式字符串: %e, %g等). 各种字符串选项在第7章[Gmsh选项](第225页)中列出. GetEnv从操作系统获取环境变量的值. GetString允许获取ONELAB字符串值(可选的第二个参数是变量不存在时返回的默认值). GetStringValue交互式地向用户请求一个值(第二个参数是非交互式模式下使用的值). StrReplace的参数为: 输入字符串, 旧子字符串, 新子字符串(在Str和Sprintf中可以使用方括号代替圆括号). Physical Point等或Point等检索物理实体或基本实体的名称(如果有). NameToString将变量名转换为字符串.
DefineString允许在一行中定义ONELAB变量. 作为第一个参数给出的字符串表达式是默认值; 后面是各种ONELAB选项. 有关更多信息, 请参见ONELAB教程wiki.
字符串表达式主要用于指定非数字选项和输入/输出文件名. 参见2.8节[t8](第33页), 了解在动画脚本中使用字符串表达式的有趣示例. 字符串表达式列表定义如下:
string-expression-list: string-expression <,...>
5.1.4. 5.1.4 颜色表达式
颜色表达式是固定长度的带括号表达式列表和字符串之间的混合:
color-expression: string-expression |
{ expression, expression, expression } | { expression, expression, expression, expression } |
color-option
第一种情况允许使用X Windows名称来引用颜色, 例如Red, SpringGreen, LavenderBlush3等(参见源代码中的src/common/Colors.h以获取完整列表). 第二种情况允许通过使用三个表达式指定颜色的红, 绿, 蓝分量(值在0到255之间)来定义颜色. 第三种情况允许通过使用红, 绿, 蓝颜色分量以及alpha通道来定义颜色. 最后一种情况允许使用color-option的值作为color-expression. 各种颜色选项在第7章[Gmsh选项](第225页)中列出.
参见2.3节[t3](第21页), 了解颜色表达式使用的示例.
5.1.5. 5.1.5 运算符
Gmsh的运算符类似于C和C++中的相应运算符. 以下是可用的一元, 二元和三元运算符列表.
operator-unary-left:
一元减号.
!
逻辑非.
operator-unary-right: ++
后增量.
--
后减量.
operator-binary: ^
幂运算.
*
乘法.
/
除法.
%
取模.
+
加法.
-
减法.
==
等于.
!=
不等于.
>
大于.
>=
大于等于.
<
小于.
<=
小于等于.
&&
逻辑" 与" .
||
逻辑" 或" . (警告: 逻辑" 或" 总是意味着两个参数都被求值. 也就是说, 与C或C++不同, 即使第一个操作数为真, ||的第二个操作数也会被求值. )
operator-ternary-left: ?
operator-ternary-right: :
唯一的三元运算符由operator-ternary-left和operator-ternary-right组成, 如果第一个参数非零, 则返回第二个参数的值; 否则返回第三个参数的值.
下面总结了求值优先级(从强到弱, 即/的求值优先级高于+). 可以在任何地方使用括号()来改变求值顺序: 1.
(), [], ., # 2. ^ 3. !, ++, –, -(一元) 4. /, /, % 5. +, - 6. <, >,
<=, >= 7. =, ! 8. && 9. || 10. ?: 11. , +, -, *, /=
5.1.6. 5.1.6 内置函数
内置函数由一个标识符后跟一对包含表达式列表的括号组成. 参数列表也可以放在括号之间, 而不是圆括号. 以下是当前实现的内置函数列表:
build-in-function: Acos ( expression )
表达式在[-1,1]中的反余弦(反余弦). 返回[0,Pi]中的值.
Asin ( expression )
表达式在[-1,1]中的反正弦(反正弦). 返回[-Pi/2,Pi/2]中的值.
Atan ( expression )
表达式的反正切(反正切). 返回[-Pi/2,Pi/2]中的值.
Atan2 ( expression, expression )
第一个表达式除以第二个表达式的反正切(反正切). 返回[-Pi,Pi]中的值.
Ceil ( expression )
将表达式向上舍入到最接近的整数.
Cos ( expression )
表达式的余弦.
Cosh ( expression )
表达式的双曲余弦.
Exp ( expression )
返回e(自然对数的底数)的表达式次幂的值.
Fabs ( expression )
表达式的绝对值.
Fmod ( expression, expression )
第一个表达式除以第二个表达式的余数, 与第一个表达式的符号相同.
Floor ( expression )
将表达式向下舍入到最接近的整数.
Hypot ( expression, expression )
返回其两个参数的平方和的平方根.
Log ( expression )
表达式的自然对数(expression>0).
Log10 ( expression )
表达式的以10为底的对数(expression>0).
Max ( expression, expression )
两个参数中的最大值.
Min ( expression, expression )
两个参数中的最小值.
Modulo ( expression, expression )
参见Fmod(expression, expression).
Rand ( expression )
0到expression之间的随机数.
Round ( expression )
将表达式四舍五入到最接近的整数.
Sqrt ( expression )
表达式的平方根(expression>=0).
Sin ( expression )
表达式的正弦.
Sinh ( expression )
表达式的双曲正弦.
Step ( expression )
如果表达式为负则返回0, 否则返回1.
Tan ( expression )
表达式的正切.
Tanh ( expression )
表达式的双曲正切.
5.1.7. 5.1.7 用户定义宏
用户定义的宏不带参数, 其求值方式就好像包含宏体的文件被包含在Call语句的位置一样.
Macro string | string-expression
开始声明一个名为string的用户定义宏. 宏体从" Macro string" 之后的行开始, 可以包含任何Gmsh命令. Macro的同义词是Function.
Return
结束当前用户定义宏的主体. 宏声明不能嵌套.
Call string | string-expression ;
执行(先前定义的)名为string的宏的主体.
参见2.5节[t5](第26页), 了解用户定义宏的示例. Gmsh脚本语言的一个缺点是所有变量都是" 公共的" . 因此, 在宏体内定义的变量也将在外部可用!
5.1.8. 5.1.8 循环和条件语句
循环和条件语句定义如下, 并且可以嵌套:
For ( expression : expression )
从第一个表达式的值迭代到第二个表达式的值, 增量为1. 在每次迭代中, 执行" For(expression:expression)" 和匹配的EndFor之间的命令.
For ( expression : expression : expression )
从第一个表达式的值迭代到第二个表达式的值, 增量为等于第三个表达式的正数或负数. 在每次迭代中, 执行" For(expression:expression:expression)" 和匹配的EndFor之间的命令.
For string In { expression : expression }
从第一个表达式的值迭代到第二个表达式的值, 增量为1. 在每次迭代中, 迭代器的值被赋予名为string的表达式, 并且执行" For string In {expression:expression}" 和匹配的EndFor之间的命令.
For string In { expression : expression : expression }
从第一个表达式的值迭代到第二个表达式的值, 增量为等于第三个表达式的正数或负数. 在每次迭代中, 迭代器的值被赋予名为string的表达式, 并且执行" For string In {expression:expression:expression}" 和匹配的EndFor之间的命令.
EndFor
结束匹配的For命令.
If ( expression )
如果表达式非零, 则求值" If(expression)" 与匹配的ElseIf, Else或EndIf之间的主体.
ElseIf ( expression )
如果表达式非零, 并且之前匹配的If和ElseIf的表达式都不为非零, 则求值" ElseIf(expression)" 与下一个匹配的ElseIf, Else或EndIf之间的主体.
Else
如果之前匹配的If和ElseIf的表达式都不为非零, 则求值Else与匹配的EndIf之间的主体.
EndIf
结束匹配的If命令.
5.1.9. 5.1.9 其他通用命令
以下命令可在Gmsh脚本中的任何位置使用:
string = expression;
创建一个新的表达式标识符string, 或将表达式赋给现有的表达式标识符. 以下表达式标识符是预定义的(硬编码在Gmsh的解析器中):
Pi
返回3.1415926535897932.
GMSH_MAJOR_VERSION
返回Gmsh的主版本号.
GMSH_MINOR_VERSION
返回Gmsh的次版本号.
GMSH_PATCH_VERSION
返回Gmsh的补丁版本号.
MPI_Size
返回Gmsh运行的处理器数量. 除非使用ENABLEMPI编译Gmsh(参见附录A[编译源代码], 第377页), 否则它始终为1.
MPI_Rank
返回当前处理器的排名.
Cpu
返回当前CPU时间(以秒为单位).
Memory
返回当前内存使用量(以Mb为单位).
TotalMemory
返回可用的总内存(以Mb为单位).
newp
返回下一个可用的点标记. 如1.1节[几何模块](第7页)所述, 每个几何点必须关联一个唯一的标记: newp允许获取已分配的最高标记(加1). 这在编写用户定义宏(参见5.1.7节[用户定义宏], 第98页)或通用几何图元时特别有用, 此时无法预先知道哪些标记已被分配, 哪些仍可用.
newc
返回下一个可用的曲线标记.
news
返回下一个可用的曲面标记.
newv
返回下一个可用的体积标记.
newcl
返回下一个可用的曲线环标记.
newsl
返回下一个可用的曲面环标记.
newreg
返回下一个可用的区域标记. 也就是说, newreg返回newp, newl, news, newv, newll, newsl和所有物理组标记中的最大值.
string = { };
创建一个具有空列表的新表达式列表标识符string.
string[] = { expression-list };
创建一个具有表达式列表的新表达式列表标识符string, 或将表达式列表赋给现有的表达式列表标识符. 也允许使用圆括号代替方括号; 尽管不推荐, 但也可以完全省略括号.
string [ { expression-list } ] = { expression-list };
将右侧表达式列表中的每个项赋给现有表达式列表标识符的元素(由左侧表达式列表索引). 两个表达式列表必须包含相同数量的项. 也可以使用圆括号代替方括号.
string += expression;
将表达式相加并赋给现有的表达式标识符.
string -= expression;
将表达式相减并赋给现有的表达式标识符.
string *= expression;
将表达式相乘并赋给现有的表达式标识符.
string /= expression;
将表达式相除并赋给现有的表达式标识符.
string += { expression-list };
将表达式列表附加到现有的表达式列表或创建一个包含表达式列表的新表达式列表.
string -= { expression-list };
从现有表达式列表中删除表达式列表中的项.
string [ { expression-list } ] += { expression-list };
逐项相加并赋值, 将右侧表达式列表赋给现有的表达式列表标识符. 也可以使用圆括号代替方括号.
string [ { expression-list } ] -= { expression-list };
逐项相减并赋值, 将右侧表达式列表赋给现有的表达式列表标识符. 也可以使用圆括号代替方括号.
string [ { expression-list } ] *= { expression-list };
逐项相乘并赋值, 将右侧表达式列表赋给现有的表达式列表标识符. 也可以使用圆括号代替方括号.
string [ { expression-list } ] /= { expression-list };
逐项相除并赋值, 将右侧表达式列表赋给现有的表达式列表标识符. 也可以使用圆括号代替方括号.
string = string-expression;
创建一个具有给定字符串表达式的新字符串表达式标识符string.
string[] = Str( string-expression-list ) ;
创建一个具有给定字符串表达式列表的新字符串表达式列表标识符string. 也可以使用圆括号代替方括号.
string[] += Str( string-expression-list ) ;
将字符串表达式列表附加到现有列表. 也可以使用圆括号代替方括号.
DefineConstant[ string = expression|string-expression <, ...>];
仅当之前未定义时, 创建一个新的表达式标识符string, 其值为expression.
DefineConstant[ string = { expression|string-expression, onelab-options } <, ...>];
与前一种情况相同, 不同之处在于, 如果变量之前未定义, 它也会与ONELAB数据库交换. 有关更多信息, 请参见ONELAB教程wiki.
SetNumber( string-expression , expression );
将数值ONELAB变量string-expression的值设置为expression.
SetString( string-expression , string-expression );
将字符串ONELAB变量string-expression的值设置为string-expression.
number-option = expression;
将表达式赋给实数选项.
string-option = string-expression;
将字符串表达式赋给字符串选项.
color-option = color-expression;
将颜色表达式赋给颜色选项.
number-option += expression;
将表达式相加并赋给实数选项.
number-option -= expression;
将表达式相减并赋给实数选项.
number-option *= expression;
将表达式相乘并赋给实数选项.
number-option /= expression;
将表达式相除并赋给实数选项.
Abort;
中止当前脚本.
Exit < expression >;
退出Gmsh(可选地使用表达式级别代替0).
CreateDir string-expression;
创建目录string-expression.
Printf ( string-expression <, expression-list> );
在信息窗口和/或终端中打印字符串表达式. Printf等同于C函数printf: string-expression是可以包含格式字符(%f, %e等)的格式字符串. 请注意, Gmsh中所有表达式都被求值为浮点值(参见5.1.2节[浮点表达式], 第91页), 因此只有有效的浮点格式字符在string-expression中有意义. 参见2.5节[t5](第26页), 了解Printf使用的示例.
Printf ( string-expression , expression-list ) > string-expression;
与上面的Printf相同, 但将表达式输出到文件中.
Printf ( string-expression , expression-list ) >> string-expression;
与上面的Printf相同, 但将表达式附加到文件末尾.
Warning|Error ( string-expression <, expression-list> );
与Printf相同, 但发出警告或错误.
Merge string-expression;
合并名为string-expression的文件. 此命令等同于GUI中的" File>Merge" 菜单. 文件的处理取决于其扩展名和/或内容: 打开包含模型数据的文件将创建一个新模型. 如果string-expression中的路径不是绝对路径, 则string-expression会附加到当前文件的路径. 此操作触发CAD模型与内部Gmsh模型的同步.
ShapeFromFile( string-expression );
合并BREP, STEP或IGES文件, 并返回最高维度实体的标记. 仅在OpenCASCADE几何内核中可用.
Draw;
重绘场景.
SplitCurrentWindowHorizontal expression;
以expression给出的比例水平分割当前窗口.
SplitCurrentWindowVertical expression;
以expression给出的比例垂直分割当前窗口.
SetCurrentWindow expression;
通过指定其在所有窗口列表中的索引(从0开始)来设置当前窗口. 当通过拆分创建新窗口时, 新窗口会附加到列表的末尾.
UnsplitWindow;
恢复为单个窗口.
SetChanged;
强制重新生成网格和后处理顶点数组. 例如, 在创建具有变化的裁剪平面的动画时很有用等.
BoundingBox;
重新计算场景的边界框(通常仅在添加新模型实体或包含或合并文件后计算). 边界框的计算如下: 1. 如果有网格(即至少一个网格节点), 则边界框取为包围所有网格节点的框; 2. 如果没有网格但有几何(即至少一个几何点), 则边界框取为包围所有几何点的框; 3. 如果没有网格和几何, 但有一些后处理视图, 则边界框取为包围视图中所有图元的框.
此操作触发CAD模型与内部Gmsh模型的同步.
BoundingBox { expression, expression, expression, expression, expression, expression };
强制场景的边界框为给定的表达式(X最小值, X最大值, Y最小值, Y最大值, Z最小值, Z最大值). 请注意, 坐标的顺序与模型实体的BoundingBox命令中的不同: 参见5.1.2节[浮点表达式](第91页).
Delete Model;
删除当前模型(所有模型实体及其关联的网格).
Delete Meshes;
删除当前模型中的所有网格.
Delete Physicals;
删除所有物理组.
Delete Variables;
删除所有表达式.
Delete Options;
删除当前选项并恢复为默认值.
Delete string;
删除表达式string.
Print string-expression;
使用当前的Print.Format(参见7.1节[通用选项], 第225页)将图形窗口打印到名为string-expression的文件中. 如果string-expression中的路径不是绝对路径, 则string-expression会附加到当前文件的路径. 此操作触发CAD模型与内部Gmsh模型的同步.
Sleep expression;
暂停Gmsh的执行expression秒.
SystemCall string-expression;
执行(阻塞)系统调用.
NonBlockingSystemCall string-expression;
执行(非阻塞)系统调用.
OnelabRun ( string-expression <, string-expression > )
运行ONELAB客户端(第一个参数是客户端名称, 第二个可选参数是命令行).
SetName string-expression;
更改当前模型的名称.
SetFactory(string-expression);
更改当前几何内核(即确定用于所有后续几何命令的CAD内核). 当前可用的内核: " Built-in" 和" OpenCASCADE" .
SyncModel;
强制从旧几何数据库立即传输到新数据库(此传输通常在读取文件后立即发生).
NewModel;
创建一个新的当前模型.
Include string-expression;
在输入文件的当前位置包含名为string-expression的文件. include命令应单独占一行. 如果string-expression中的路径不是绝对路径, 则string-expression会附加到当前文件的路径.
5.2. 5.2 几何脚本命令
通过在几何脚本命令之前分别指定SetFactory("Built-in")或SetFactory("OpenCASCADE"), 可以在脚本语言中使用内置和OpenCASCADE CAD内核. 如果未指定SetFactory, 则使用内置内核.
可以使用自底向上的边界表示方法, 首先定义点(使用Point命令), 然后是曲线(使用Line, Circle, Spline等命令或通过挤压点), 然后是曲面(例如使用Plane Surface或Surface命令, 或通过挤压曲线), 最后是体积(使用Volume命令或通过挤压曲面). 然后可以以各种方式操作实体, 例如使用Translate, Rotate, Scale或Symmetry命令. 如果没有更高维度的实体引用它们, 可以使用Delete命令删除它们. 使用OpenCASCADE内核, 可以使用额外的布尔运算: BooleanIntersection, BooleanUnion, BooleanDifference和BooleanFragments.
下一小节描述脚本语言中所有可用的几何命令. 请注意, 定义模型实体遵循以下一般规则: 如果表达式定义了一个新实体, 则用括号括起来. 如果表达式引用先前定义的实体, 则用大括号括起来.
5.2.1. 5.2.1 点
Point ( expression ) = { expression, expression, expression <, expression > };
创建一个点. 括号内的表达式是点的标记; 右侧大括号内的前三个表达式给出三维欧几里得空间中点的三个X, Y和Z坐标; 可选的最后一个表达式设置该点的指定网格单元大小. 有关此值如何在网格划分过程中使用的更多信息, 请参见1.2.2节[指定网格单元大小](第10页).
Physical Point ( expression | string-expression <, expression> ) <+|->= { expression-list };
创建一个物理点. 括号内的表达式是物理点的标记; 右侧的表达式列表应包含需要分组到物理点内的所有基本点的标记. 如果在括号内给出字符串表达式而不是表达式, 则将字符串标签与物理标记相关联, 该物理标记可以显式提供(在逗号后)或不提供(在这种情况下, 会自动创建唯一标记).
5.2.2. 5.2.2 曲线
Line ( expression ) = { expression, expression };
创建直线段. 括号内的表达式是线段的标记; 右侧大括号内的两个表达式给出线段的起点和终点的标记.
Bezier ( expression ) = { expression-list };
创建贝塞尔曲线. 表达式列表包含控制点的标记.
BSpline ( expression ) = { expression-list };
创建三次B样条曲线. 表达式列表包含控制点的标记. 如果第一个点和最后一个点相同, 则创建周期性曲线.
Spline ( expression ) = { expression-list };
创建一条通过表达式列表中的点的样条曲线. 使用内置几何内核时, 这会构造一条Catmull-Rom样条曲线. 使用OpenCASCADE内核时, 这会构造一条C2 B样条曲线. 如果第一个点和最后一个点相同, 则创建周期性曲线.
Circle ( expression ) = { expression, expression, expression <, ...> };
创建圆弧. 如果右侧提供三个表达式, 则它们定义圆弧的起点, 中心和终点. 使用内置几何内核时, 圆弧应严格小于Pi. 使用OpenCASCADE内核时, 如果提供4到6个表达式, 则前三个定义中心的坐标, 下一个定义半径, 可选的下两个定义起始角和终止角.
Ellipse ( expression ) = { expression, expression, expression <, ...> };
创建椭圆弧. 如果右侧提供四个表达式, 则它们定义起点, 中心点, 长轴上的任意一点和终点. 如果第一个点是长轴点, 则可以省略第三个表达式. 使用OpenCASCADE内核时, 如果提供5到7个表达式, 则前三个定义中心的坐标, 下两个定义长半径(沿x轴)和短半径(沿y轴), 下两个定义起始角和终止角. 请注意, OpenCASCADE不允许创建长半径小于短半径的椭圆弧.
Compound Spline | BSpline ( expression ) = { expression-list } Using expression;
根据在表达式列表中的曲线上采样的控制点创建样条曲线或B样条曲线. Using expression指定每条曲线上用于计算采样点的间隔数. 复合样条和B样条仅在built-in几何内核中可用.
Curve Loop ( expression ) = { expression-list };
创建有向曲线环, 即闭合线框. 括号内的表达式是曲线环的标记; 右侧的表达式列表应包含构成曲线环的所有曲线的标记. 曲线环必须是闭合环. 使用内置几何内核时, 曲线应按顺序和方向排列, 使用负标记指定反向方向. (如果方向正确但顺序错误, Gmsh实际上会在内部重新排序列表以创建一致的环; 内置内核还支持在单个Curve Loop命令中使用多个曲线环(或子环), 但不推荐这样做). 使用OpenCASCADE内核时, 曲线环总是根据其第一条曲线的方向定向; 可以指定负标记以与内置内核兼容, 但会被简单地忽略. 曲线环用于创建曲面: 参见5.2.3节[曲面](第106页).
Wire ( expression ) = { expression-list };
创建由曲线组成的路径. Wire仅在OpenCASCADE内核中可用. 它们用于创建ThruSections和沿路径的挤压.
Physical Curve ( expression | string-expression <, expression> ) <+|->= { expression-list };
创建物理曲线. 括号内的表达式是物理曲线的标记; 右侧的表达式列表应包含需要分组到物理曲线内的所有基本曲线的标记. 如果在括号内给出字符串表达式而不是表达式, 则将字符串标签与物理标记相关联, 该物理标记可以显式提供(在逗号后)或不提供(在这种情况下, 会自动创建唯一标记). 在某些网格文件格式(例如MSH2)中, 在表达式列表中指定负标记将反转保存的网格文件中属于相应基本曲线的网格元素的方向.
5.2.3. 5.2.3 曲面
Plane Surface ( expression ) = { expression-list };
创建平面曲面. 括号内的表达式是平面曲面的标记; 右侧的表达式列表应包含定义曲面的所有曲线环的标记. 第一个曲线环定义曲面的外边界; 所有其他曲线环定义曲面中的孔. 定义孔的曲线环不应与外曲线环有任何共同的曲线(在这种情况下, 它不是孔, 应该分别定义两个曲面). 同样, 定义同一曲面中孔的曲线环不应与另一个定义孔的曲线环有任何共同的曲线(在这种情况下, 应该合并两个曲线环).
Surface ( expression ) = { expression-list } < In Sphere { expression }, Using Point { expression-list } >;
创建曲面填充. 使用内置内核时, 第一个曲线环应包含三个或四个曲线, 曲面使用超限插值构造, 可选的In Sphere参数强制曲面为球面补丁(额外参数给出球中心的标记). 使用OpenCASCADE内核时, 通过优化构造B样条曲面以匹配边界曲线, 以及Using Point之后提供的(可选)点.
BSpline Surface ( expression ) = { expression-list };
创建B样条曲面填充. 只能提供由2, 3或4条B样条曲线组成的单个曲线环. BSpline Surface仅在OpenCASCADE内核中可用.
Bezier Surface ( expression ) = { expression-list };
创建贝塞尔曲面填充. 只能提供由2, 3或4条贝塞尔曲线组成的单个曲线环. Bezier Surface仅在OpenCASCADE内核中可用.
Disk ( expression ) = { expression-list };
创建圆盘. 当右侧提供四个表达式(中心的3个坐标和半径)时, 圆盘是圆形的. 第五个表达式定义Y方向的半径, 形成椭圆. Disk仅在OpenCASCADE内核中可用.
Rectangle ( expression ) = { expression-list };
创建矩形. 前3个表达式定义左下角; 接下来的2个定义宽度和高度. 如果提供第6个表达式, 它定义圆角矩形的半径. Rectangle仅在OpenCASCADE内核中可用.
Surface Loop ( expression ) = { expression-list } < Using Sewing >;
创建曲面环(壳). 括号内的表达式是曲面环的标记; 右侧的表达式列表应包含构成曲面环的所有曲面的标记. 曲面环必须始终表示闭合的壳, 并且曲面应以一致的方式定向(使用负标记指定反向定向). (曲面环用于创建体积: 参见5.2.4节[体积], 第107页). 使用OpenCASCADE内核时, 可选的Using Sewing参数允许构建由共享几何上相同(但拓扑上不同)曲线的曲面组成的壳.
Physical Surface ( expression | string-expression <, expression> ) <+|->= { expression-list };
创建物理曲面. 括号内的表达式是物理曲面的标记; 右侧的表达式列表应包含需要分组到物理曲面内的所有基本曲面的标记. 如果在括号内给出字符串表达式而不是表达式, 则将字符串标签与物理标记相关联, 该物理标记可以显式提供(在逗号后)或不提供(在这种情况下, 会自动创建唯一标记). 在某些网格文件格式(例如MSH2)中, 在表达式列表中指定负标记将反转保存的网格文件中属于相应基本曲面的网格元素的方向.
5.2.4. 5.2.4 体积
Volume ( expression ) = { expression-list };
创建体积. 括号内的表达式是体积的标记; 右侧的表达式列表应包含定义体积的所有曲面环的标记. 第一个曲面环定义体积的外边界; 所有其他曲面环定义体积中的孔. 定义孔的曲面环不应与外曲面环有任何共同的曲面(在这种情况下, 它不是孔, 应该分别定义两个体积). 同样, 定义同一体积中孔的曲面环不应与另一个定义孔的曲面环有任何共同的曲面(在这种情况下, 应该合并两个曲面环).
Sphere ( expression ) = { expression-list };
创建球体, 由其中心的3个坐标和半径定义. 附加表达式定义3个角度限制. 前两个可选参数定义极角范围(从-Pi/2到Pi/2). 可选的" angle3" 参数定义方位角范围(从0到2*Pi). Sphere仅在OpenCASCADE内核中可用.
Box ( expression ) = { expression-list };
创建盒子, 由一个点的3个坐标和3个范围定义. Box仅在OpenCASCADE内核中可用.
Cylinder ( expression ) = { expression-list };
创建圆柱体, 由第一个圆形面中心的3个坐标, 定义其轴的向量的3个分量及其半径定义. 附加表达式定义角度范围. Cylinder仅在OpenCASCADE内核中可用.
Torus ( expression ) = { expression-list };
创建圆环, 由其中心的3个坐标和2个半径定义. 附加表达式定义角度范围. Torus仅在OpenCASCADE内核中可用.
Cone ( expression ) = { expression-list };
创建圆锥体, 由第一个圆形面中心的3个坐标, 定义其轴的向量的3个分量以及面的两个半径(这些半径可以为零)定义. 附加表达式定义角度范围. Cone仅在OpenCASCADE内核中可用.
Wedge ( expression ) = { expression-list };
创建直角楔体, 由直角点的3个坐标和3个范围定义. 附加参数定义顶部X范围(默认为零). Wedge仅在OpenCASCADE内核中可用.
ThruSections ( expression ) = { expression-list };
创建通过曲线环定义的体积. ThruSections仅在OpenCASCADE内核中可用.
Ruled ThruSections ( expression ) = { expression-list };
与ThruSections相同, 但边界上创建的曲面被强制为直纹面. Ruled ThruSections仅在OpenCASCADE内核中可用.
Physical Volume ( expression | string-expression <, expression> ) <+|->= { expression-list };
创建物理体积. 括号内的表达式是物理体积的标记; 右侧的表达式列表应包含需要分组到物理体积内的所有基本体积的标记. 如果在括号内给出字符串表达式而不是表达式, 则将字符串标签与物理标记相关联, 该物理标记可以显式提供(在逗号后)或不提供(在这种情况下, 会自动创建唯一标记).
5.2.5. 5.2.5 挤压
曲线, 曲面和体积也可以分别通过点, 曲线和曲面的挤压来创建. 以下是几何挤压命令的语法(请转到5.3.2节[结构化网格], 第113页, 查看如何扩展这些命令以同时挤压网格):
extrude:
Extrude { expression-list } { extrude-list }
使用平移挤压extrude-list中的所有基本实体(点, 曲线或曲面). 表达式列表应包含三个表达式, 给出平移向量的X, Y和Z分量.
Extrude { { expression-list }, { expression-list }, expression } { extrude-list }
使用旋转挤压extrude-list中的所有基本实体(点, 曲线或曲面). 第一个表达式列表应包含三个表达式, 给出旋转轴的X, Y和Z方向; 第二个表达式列表应包含三个表达式, 给出该轴上任意一点的X, Y和Z分量; 最后一个表达式应包含旋转角度(以弧度为单位). 使用内置几何内核时, 角度应严格小于Pi.
Extrude { { expression-list }, { expression-list }, { expression-list }, expression } { extrude-list }
使用平移结合旋转(产生" 扭曲" )挤压extrude-list中的所有基本实体(点, 曲线或曲面). 第一个表达式列表应包含三个表达式, 给出平移向量的X, Y和Z分量; 第二个表达式列表应包含三个表达式, 给出旋转轴的X, Y和Z方向, 该方向应与平移方向匹配; 第三个表达式列表应包含三个表达式, 给出该轴上任意一点的X, Y和Z分量; 最后一个表达式应包含旋转角度(以弧度为单位). 使用内置几何内核时, 角度应严格小于Pi.
Extrude { extrude-list }
沿其法线方向挤压extrude-list中的实体. 仅在内置几何内核中可用.
Extrude { extrude-list } Using Wire { expression-list }
沿给定的线框挤压extrude-list中的实体. 仅在OpenCASCADE几何内核中可用.
ThruSections { expression-list }
通过给定的曲线环或线框创建曲面. ThruSections仅在OpenCASCADE内核中可用.
Ruled ThruSections { expression-list }
通过给定的曲线环或线框创建直纹曲面. Ruled ThruSections仅在OpenCASCADE内核中可用.
Fillet { expression-list } { expression-list } { expression-list }
在一些曲线(第二个列表)上对体积(第一个列表)进行倒圆, 使用提供的半径(第三个列表). 半径列表可以包含单个半径, 与曲线数量相同的半径, 或者是曲线数量的两倍(在这种情况下, 为曲线的起点和终点提供不同的半径). Fillet仅在OpenCASCADE内核中可用.
Chamfer { expression-list } { expression-list } { expression-list } { expression-list }
在一些曲线(第二个列表)上对体积(第一个列表)进行倒角, 使用在给定曲面(第三个列表)上测量的提供的距离(第四个列表). 距离列表可以包含单个距离, 与曲线数量相同的距离, 或者是曲线数量的两倍(在这种情况下, 每对中的第一个距离在给定的相应曲面上测量). Chamfer仅在OpenCASCADE内核中可用.
其中:
extrude-list: <Physical> Point | Curve | Surface { expression-list-or-all }; ...
如5.1.2节[浮点表达式](第91页)中所述, extrude可用于表达式, 在这种情况下, 它返回一个标记列表. 默认情况下, 列表包含索引0处的挤压实体的" 顶部" 和索引1处的挤压实体, followed by the " sides" of the extruded entity at indices 2, 3, etc. 例如:
Point(1) = {0,0,0}; Point(2) = {1,0,0};
Line(1) = {1, 2};
out[] = Extrude{0,1,0}{ Curve{1}; };
Printf("top curve = %g", out[0]); Printf("surface = %g", out[1]);
Printf("side curves = %g and %g", out[2], out[3]);
此行为可以通过Geometry.ExtrudeReturnLateralEntities选项更改(参见7.3节[几何选项], 第252页).
5.2.6. 5.2.6 布尔运算
布尔运算可以应用于曲线, 曲面和体积. 所有布尔运算都作用于两个基本实体列表. 第一个列表表示对象; 第二个列表表示工具. 布尔运算的一般语法如下:
boolean:
BooleanIntersection { boolean-list } { boolean-list }
计算对象和工具的交集.
BooleanUnion { boolean-list } { boolean-list }
计算对象和工具的并集.
BooleanDifference { boolean-list } { boolean-list }
从对象中减去工具.
BooleanFragments { boolean-list } { boolean-list }
计算对象和工具中的实体相交产生的所有片段, 使所有界面共形. 当应用于不同维度的实体时, 如果低维度实体不在高维度实体的边界上, 它们将自动嵌入高维度实体中.
其中:
boolean-list:
<Physical> Curve | Surface | Volume { expression-list-or-all }; ... | Delete ;
如果在boolean-list中指定Delete, 则删除工具和/或对象.
如5.1.2节[浮点表达式](第91页)中所述, boolean可用于表达式, 在这种情况下, 它返回由布尔运算创建的最高维度实体的标记列表. 参见examples/boolean中的示例.
布尔运算还有另一种语法, 当预先知道运算将产生单个(最高维度)实体时可以使用:
boolean-explicit:
BooleanIntersection ( expression ) = { boolean-list } { boolean-list };
计算对象和工具的交集, 并为结果分配标记表达式.
BooleanUnion ( expression ) = { boolean-list } { boolean-list };
计算对象和工具的并集, 并为结果分配标记表达式.
BooleanDifference ( expression ) = { boolean-list } { boolean-list };
从对象中减去工具, 并为结果分配标记表达式.
同样, 参见examples/boolean中的示例.
布尔运算仅在OpenCASCADE几何内核中可用.
5.2.7. 5.2.7 变换
几何变换可以应用于基本实体, 或基本实体的副本(使用Duplicata命令: 见下文). 变换命令的语法为:
transform:
Dilate { { expression-list }, expression } { transform-list }
将transform-list中的所有基本实体按因子expression缩放. 表达式列表应包含三个表达式, 给出均匀缩放变换中心的X, Y和Z坐标.
Dilate { { expression-list }, { expression, expression, expression } } { transform-list }
使用沿X, Y和Z的不同因子(三个表达式)缩放transform-list中的所有基本实体. 表达式列表应包含三个表达式, 给出均匀缩放变换中心的X, Y和Z坐标.
Rotate { { expression-list }, { expression-list }, expression } { transform-list }
将transform-list中的所有基本实体旋转expression弧度. 第一个表达式列表应包含三个表达式, 给出旋转轴的X, Y和Z方向; 第二个表达式列表应包含三个表达式, 给出该轴上任意一点的X, Y和Z分量.
Symmetry { expression-list } { transform-list }
将所有基本实体对称变换到一个平面. 表达式列表应包含四个表达式, 给出平面方程的系数.
Affine { expression-list } { transform-list }
将4x4仿射变换矩阵(按行给出16个条目; 为方便起见, 只能提供12个)应用于所有基本实体. 目前仅在OpenCASCADE内核中可用.
Translate { expression-list } { transform-list }
平移transform-list中的所有基本实体. 表达式列表应包含三个表达式, 给出平移向量的X, Y和Z分量.
Boundary { transform-list }
(本身不是变换. )返回transform-list中基本实体边界上的实体, 其符号指示它们在边界中的方向. 要获取无符号标记(例如, 在其他命令中重用输出), 请对返回的列表应用Abs函数. 此操作触发CAD模型与内部Gmsh模型的同步.
CombinedBoundary { transform-list }
(本身不是变换. )返回基本实体的边界, 合并为单个实体, 在transform-list中. 用于计算复杂零件的边界很有用. 此操作触发CAD模型与内部Gmsh模型的同步.
PointsOf { transform-list }
(本身不是变换. )返回基本实体边界上的所有几何点. 用于计算复杂零件的边界很有用. 此操作触发CAD模型与内部Gmsh模型的同步.
Intersect Curve { expression-list } Surface { expression }
(本身不是变换. )返回表达式列表中给出的曲线与指定曲面的交点. 目前仅在built-in内核中可用.
Split Curve { expression } Point { expression-list }
(本身不是变换. )在指定的控制点上分割曲线表达式. 仅在内置内核中可用, 用于样条和B样条.
其中:
transform-list: <Physical> Point | Curve | Surface | Volume { expression-list-or-all }; ... | Duplicata { <Physical> Point | Curve | Surface | Volume { expression-list-or-all }; ... } | transform
5.2.8. 5.2.8 其他几何命令
以下是当前可用的所有其他几何命令的列表:
Coherence;
删除所有重复的基本实体(例如, 具有相同坐标的点). 请注意, 使用内置几何内核时, Gmsh会在每次几何变换后自动执行Coherence命令, 除非Geometry.AutoCoherence设置为零(参见7.3节[几何选项], 第252页). 使用OpenCASCADE几何内核时, Coherence只是对所有实体执行BooleanFragments操作的快捷方式, 并对所有操作数应用Delete运算符.
HealShapes;
应用形状修复程序, 根据Geometry.OCCFixDegenerated, Geometry.OCCFixSmallEdges, Geometry.OCCSewFaces, Geometry.OCCMakeSolids, Geometry.OCCFixSmallFaces. 仅在OpenCASCADE几何内核中可用.
< Recursive > Delete { <Physical> Point | Curve | Surface | Volume { expression-list-or-all }; ... }
删除其标记在expression-list-or-all中给出的所有基本实体. 如果一个实体链接到另一个实体(例如, 如果一个点用作曲线的控制点), Delete没有效果(必须先删除曲线才能删除点). Recursive变体删除实体及其所有低维度的子实体. 此操作触发CAD模型与内部Gmsh模型的同步.
Delete Embedded { <Physical> Point | Curve | Surface | Volume { expression-list-or-all }; ... }
删除在expression-list-or-all中给出的基本实体中的所有嵌入实体. 此操作触发CAD模型与内部Gmsh模型的同步.
SetMaxTag Point | Curve | Surface | Volume ( expression )
将实体类别的最大标记强制为给定值, 以便同一类别中随后创建的实体的标记不会小于给定值.
< Recursive > Hide { <Physical> Point | Curve | Surface | Volume { expression-list-or-all }; ... }
隐藏expression-list-or-all中列出的实体.
Hide { : }
隐藏所有实体.
< Recursive > Show { <Physical> Point | Curve | Surface | Volume { expression-list-or-all }; ... }
显示expression-list-or-all中列出的实体.
Show { : }
显示所有实体.
Sphere | PolarSphere ( expression ) = {expression, expression};
将内置几何内核使用的当前(曲面)几何更改为(极地)球体, 由右侧指定的两个点标记定义. 左侧括号之间的表达式为此几何指定一个新的唯一标记.
Parametric Surface ( expression ) = "string" "string" "string";
将内置几何内核使用的当前(曲面)几何更改为由三个字符串表达式定义的参数曲面, 这些表达式求值为x, y和z坐标. 左侧括号之间的表达式为此几何指定一个新的唯一标记.
Coordinates Surface expression;
将内置几何内核使用的当前(曲面)几何更改为由给定表达式标识的几何.
Euclidian Coordinates ;
恢复内置几何内核的默认平面几何.
5.3. 5.3 网格脚本命令
网格模块脚本命令允许修改网格单元大小和指定结构化网格参数. 某些网格操作(例如" 网格所有曲面" )也可以在脚本文件中指定, 但通常在GUI或命令行中执行(参见第3章[Gmsh图形用户界面], 第79页和第4章[Gmsh命令行界面], 第85页).
5.3.1. 5.3.1 网格单元大小
以下是与网格单元大小规范相关的网格命令:
MeshSize { expression-list } = expression;
修改表达式列表中列出的点的指定网格单元大小. 新值由表达式给出.
Field[expression] = string;
创建一个新的场(带有标记表达式), 类型为string.
Field[expression].string = string-expression | expression | expression-list;
设置第expression个场的选项string.
Background Field = expression;
选择第expression个场作为用于计算单元大小的场. 只能给出一个背景场; 如果要组合多个场, 请使用Min或Max场(见下文).
5.3.2. 5.3.2 结构化网格
Extrude { expression-list } { extrude-list layers }
使用平移挤压几何和网格(参见5.2.5节[挤压], 第108页). layers选项确定如何挤压网格, 其语法如下:
layers: Layers { expression } | Layers { { expression-list }, { expression-list } } |
Recombine < expression >; ...
QuadTriNoNewVerts <RecombLaterals>; | QuadTriAddVerts <RecombLaterals>; ...
在第一种Layers形式中, expression给出(单个)层中要创建的单元数量. 在第二种形式中, 第一个表达式列表定义每个挤压层中应创建的单元数量, 第二个表达式列表给出每个层的归一化高度(该列表应包含一系列n个数字0 < h1 < h2 < … < hn <= 1). 参见2.3节[t3](第21页)中的示例. 对于曲线挤压, Recombine选项将在可能时将三角形重组为四边形. 对于曲面挤压, Recombine选项将在可能时将四面体重组为棱柱, 六面体或棱锥.
请注意, 从Gmsh 2.0开始, 区域标记不能再在Layers命令中显式指定. 相反, 与所有其他几何命令一样, 必须使用挤压命令自动创建的实体标识符. 例如, 以下挤压命令将在num[0]中返回新" 顶部" 曲面的标记, 在num[1]中返回新体积的标记:
num[] = Extrude {0,0,1} { Surface{1}; Layers{10}; };
QuadTriNoNewVerts和QuadTriAddVerts允许通过将共享四面体体积的边界曲面上的任何四边形细分为三角形, 将包含四边形面单元的结构化挤压体积连接到结构化或非结构化四面体体积. (它们对1D或2D挤压无效. )QuadTriNoNewVerts将任何接触这些边界三角形的区域的四面条3D单元细分为棱锥, 棱柱或四面体(必要时), 所有这些都无需添加新节点. QuadTriAddVerts以类似的方式工作, 但通过在每个单元内部的节点中心添加一个新节点来细分接触边界三角形的3D单元. 这两种方法都会产生结构化挤压, 其外层细分单元将内部未修改的单元与三角形网格区域边界连接起来.
在某些罕见情况下, 由于某些横向边界条件, 使用QuadTriNoNewVerts可能无法在不添加额外节点的情况下进行有效的单元细分. 在这种情况下, 会在单元的节点中心创建一个内部节点. 然后使用该节点分割单元. 当使用QuadTriNoNewVerts创建内部节点时, 会为每个实例发送警告消息提醒用户; 但是, 网格仍然有效且共形.
QuadTriNoNewVerts和QuadTriAddVerts可以互换使用, 但QuadTriAddVerts通常会提供更好的单元质量.
如果用户希望将结构化挤压与四面体体积连接而不修改原始结构化网格, 用户可以在结构化几何周围创建专用的界面体积, 并仅对这些体积应用QuadTri算法.
Extrude { { expression-list }, { expression-list }, expression } { extrude-list layers }
使用旋转挤压几何和网格(参见5.2.5节[挤压], 第108页). layers选项的定义如上. 使用内置几何内核时, 角度应严格小于Pi. 使用OpenCASCADE内核时, 角度应严格小于2 Pi.
Extrude { { expression-list }, { expression-list }, { expression-list }, expression } { extrude-list layers }
使用组合平移和旋转挤压几何和网格(参见5.2.5节[挤压], 第108页). layers选项的定义如上. 使用内置几何内核时, 角度应严格小于Pi. 使用OpenCASCADE内核时, 角度应严格小于2 Pi.
Extrude { Surface { expression-list }; layers < Using Index[expr]; > < Using View[expr]; > < ScaleLastLayer; > }
从指定的曲面挤压" 拓扑" 边界层. 如果未指定视图, 则边界层实体的网格使用高洛德着色(平滑)法向场创建. 如果指定了标量视图, 它会局部规定层的厚度. 如果指定了向量值视图, 它会局部规定挤压方向和厚度. 指定边界层索引允许挤压多个独立的边界层(具有独立的法向平滑). ScaleLastLayer将每个法向挤压的最后(顶部)层的高度按包含源节点的所有源单元中边的平均长度缩放(实际上, 每个单元的平均值的平均值-–—实际接触源节点的边被计算两次). 这允许最后一层的高度随源单元的大小变化, 以获得更好的单元质量. 例如, 在使用Layers定义" Layers{{1,4,2}, {0.5,0.6,1.6}}" 挤压的边界层中, 与整体平均边长为5.0的单元相邻的源节点将挤压为最后一层高度=(1.6-0.6)*5.0 (=5.0). 拓扑边界层仅在内置内核中可用. 参见sphereboundarylayer.geo或sphereboundarylayerfromview.geo获取" .geo" 文件示例, 以及aneurysm.py获取API示例.
这种方法的优点是它提供了边界层的拓扑描述, 这意味着它可以与其他几何实体连接. 缺点是网格只是" 简单" 挤压: 没有扇形, 没有对凹角的特殊处理等. 目前通过BoundaryLayer场可以使用另一种边界层算法(参见1.2.2节[指定网格单元大小], 第10页). 然而, 它仅在2D中工作, 并且是一种网格约束: 它直接在网格级别工作, 不创建几何实体. 例如, 参见BL0.geo或naca122d.geo.
Transfinite Curve { expression-list-or-all } = expression < Using Progression | Bump expression >;
选择表达式列表中的曲线使用1D超限算法进行网格划分. 右侧的表达式给出将在曲线上创建的节点数量(这会覆盖任何其他网格单元大小规定-–—参见1.2.2节[指定网格单元大小], 第10页). 可选参数" Using Progression expression" 指示超限算法按照几何级数分布节点(例如, Progression 2意味着系列中的每个线单元将是前一个的两倍长). 可选参数" Using Bump expression" 指示超限算法在曲线的两端进行细化分布节点. 此操作触发CAD模型与内部Gmsh模型的同步.
Transfinite Surface { expression-list-or-all } < = { expression-list } > < Left | Right | Alternate | AlternateRight | AlternateLeft > ;
选择曲面使用2D超限算法进行网格划分. 右侧的表达式列表应包含曲面上定义超限插值角点的三个或四个点的标记. 如果未给出标记, 超限算法将尝试自动找到角点. 可选参数指定网格不重组时三角形的定向方式. Alternate是AlternateRight的同义词. 对于3边曲面, 可以通过将Mesh.TransfiniteTri设置为1来使用特定算法生成结构化三角形. 示例可以在benchmarks/transfinite中找到. 此操作触发CAD模型与内部Gmsh模型的同步.
Transfinite Volume { expression-list } < = { expression-list } > ;
6. 7 Gmsh 选项
本章列出了 Gmsh 的所有选项. 可以在脚本文件中指定选项 (参见第 5.1 节 [通用脚本命令], 第 91 页) 或使用 API (参见第 6.2 节 [命名空间 gmsh/option], 第 128 页): 参见第 2.3 节 [t3], 第 21 页中的示例. 也可以在命令行中使用 `-setnumber` 和 `-setstring` 开关指定它们: 参见第 4 章 [Gmsh 命令行界面], 第 85 页. 许多选项也可以在 GUI 中交互式更改 (参见第 3 章 [Gmsh 图形用户界面], 第 79 页): 要查看哪个选项对应于 GUI 中的哪个小部件, 请将鼠标悬停在小部件上, 此时将出现带有选项名称的工具提示. 请注意, 某些选项可以实时影响 GUI: 例如, 加载设置 `General.GraphicsWidth` 的脚本文件 (参见第 7.1 节 [常规选项], 第 225 页) 将在运行时更改图形窗口的宽度.
Gmsh 的默认行为是在每次关闭 Gmsh 时将其中一些选项保存在每个用户的“会话资源”文件中 (参见下文选项描述中的 “保存在: General.SessionFileName”). 这例如允许自动记住窗口的大小和位置或要使用的字体. 第二组选项可以 (通过 ‘File->Save Options As Default’ 菜单自动或手动) 保存在每个用户的“选项”文件中 (参见下文列表中的 “保存在: General.OptionsFileName”), Gmsh 每次启动时都会自动加载. 最后, 其他选项只能通过使用 ‘File->Export’ 显式保存选项文件, 或使用 ‘File->Save Model Options’ 保存每个模型的选项来手动保存到磁盘 (参见列表中 “保存在: -”). 每个模型的选项保存在一个与模型文件匹配的文件名中, 但附加了 `.opt` 扩展名: 打开模型文件后, 选项文件也将被自动打开.
Gmsh 将首先尝试在 `$GMSHHOME` 目录中, 然后在 `$APPDATA` (在 Windows 上) 或 `$HOME` (在其他操作系统上), 接着在 `$TMP`, 最后在 `$TEMP` 中按此顺序保存和加载会话和选项文件. 如果这些变量都未定义, Gmsh 将尝试从当前工作目录保存/加载文件.
要将所有选项重置为其默认值, 可以手动删除 `General.SessionFileName` 和 `General.OptionsFileName` 文件, 使用 ‘Help->Restore All Options to Default Settings’, 或单击 ‘Tools->Options->General->Advanced’ 窗口中的 ‘Restore all options to default settings’ 按钮.
6.1. 7.1 常规选项
General.AxesFormatX X 轴的数字格式 (标准 C 格式) 默认值: "%.3g" 保存在: General.OptionsFileName
General.AxesFormatY Y 轴的数字格式 (标准 C 格式) 默认值: "%.3g" 保存在: General.OptionsFileName
General.AxesFormatZ Z 轴的数字格式 (标准 C 格式) 默认值: "%.3g" 保存在: General.OptionsFileName
General.AxesLabelX X 轴标签 默认值: "" 保存在: General.OptionsFileName
General.AxesLabelY Y 轴标签 默认值: "" 保存在: General.OptionsFileName
General.AxesLabelZ Z 轴标签 默认值: "" 保存在: General.OptionsFileName
General.BackgroundImageFileName JPEG, PNG 或 PDF 格式的背景图像文件 默认值: "" 保存在: General.OptionsFileName
General.BuildInfo Gmsh 构建信息 (只读) 默认值: "Version: 4.14.0-git-697fde2e8; License: GNU General Public License; Build OS: MacOSARM-sdk; Build date: 20250702; Build host: MacBook-Pro-M2-3.local; Build options: 64Bit ALGLIB[contrib] ANN[contrib] Bamg Blas[petsc] Blossom Cairo Cgns DIntegration Dlopen DomHex Eigen[contrib] Fltk GMP Gmm[contrib] Hxt Jpeg Kbipack Lapack[petsc] MathEx[contrib] Med Mesh Metis[contrib] Mmg Mpeg Netgen Nii2mesh ONELAB ONELABMetamodel OpenCASCADE OpenCASCADE-CAF OpenGL OpenMP[Homebrew] OptHom PETSc Parser Plugins Png Post QuadMeshingTools QuadTri Solver TetGen/BR TinyXML2[contrib] TouchBar Untangle Voro++[contrib] WinslowUntangler Zlib tinyobjloader; FLTK version: 1.5.0; PETSc version: 3.23.0 (complex arithmtic); OCC version: 8.0.0; MED version: 4.1.1; Packaged by: geuzaine; Web site: https://gmsh.info; Issue tracker: https://gitlab.onelab.info/gmsh/gmsh/issues" 保存在: -
General.BuildOptions Gmsh 构建选项 (只读) 默认值: "64Bit ALGLIB[contrib] ANN[contrib] Bamg Blas[petsc] Blossom Cairo Cgns DIntegration Dlopen DomHex Eigen[contrib] Fltk GMP Gmm[contrib] Hxt Jpeg Kbipack Lapack[petsc] MathEx[contrib] Med Mesh Metis[contrib] Mmg Mpeg Netgen Nii2mesh ONELAB ONELABMetamodel OpenCASCADE OpenCASCADE-CAF OpenGL OpenMP[Homebrew] OptHom PETSc Parser Plugins Png Post QuadMeshingTools QuadTri Solver TetGen/BR TinyXML2[contrib] TouchBar Untangle Voro++[contrib] WinslowUntangler Zlib tinyobjloader" 保存在: -
General.DefaultFileName 默认项目文件名 默认值: "untitled.geo" 保存在: General.OptionsFileName
General.Display 要使用的 X 服务器 (仅限 Unix 版本) 默认值: "" 保存在: -
General.ErrorFileName 如果发生致命错误, 日志保存到的文件 默认值: ".gmsh-errors" 保存在: General.OptionsFileName
General.ExecutableFileName Gmsh 可执行文件的文件名 (只读) 默认值: "" 保存在: General.SessionFileName
General.FileName 当前项目文件名 (只读) 默认值: "" 保存在: -
General.FltkTheme FLTK 用户界面主题 (例如尝试 plastic 或 gtk+) 默认值: "" 保存在: General.SessionFileName
General.GraphicsFont 图形窗口中使用的字体 默认值: "Helvetica" 保存在: General.OptionsFileName
General.GraphicsFontEngine 设置图形字体引擎 (Native, StringTexture, Cairo) 默认值: "Native" 保存在: General.OptionsFileName
General.GraphicsFontTitle 图形窗口中用于标题的字体 默认值: "Helvetica" 保存在: General.OptionsFileName
General.LogFileName 所有消息保存到的日志文件名 默认值: "" 保存在: General.OptionsFileName
General.NumberFormat 数字格式 (标准 C 格式) 默认值: "%.3g" 保存在: General.OptionsFileName
General.OptionsFileName 通过 ‘Tools->Options->Save’ 创建的选项文件; 启动时自动读取 默认值: ".gmsh-options" 保存在: General.SessionFileName
General.RecentFile0 最近打开的文件 默认值: "untitled.geo" 保存在: General.SessionFileName
General.RecentFile1 第二最近打开的文件 默认值: "untitled.geo" 保存在: General.SessionFileName
General.RecentFile2 第三最近打开的文件 默认值: "untitled.geo" 保存在: General.SessionFileName
General.RecentFile3 第四最近打开的文件 默认值: "untitled.geo" 保存在: General.SessionFileName
General.RecentFile4 第五最近打开的文件 默认值: "untitled.geo" 保存在: General.SessionFileName
General.RecentFile5 第六最近打开的文件 默认值: "untitled.geo" 保存在: General.SessionFileName
General.RecentFile6 第七最近打开的文件 默认值: "untitled.geo" 保存在: General.SessionFileName
General.RecentFile7 第八最近打开的文件 默认值: "untitled.geo" 保存在: General.SessionFileName
General.RecentFile8 第九最近打开的文件 默认值: "untitled.geo" 保存在: General.SessionFileName
General.RecentFile9 第十最近打开的文件 默认值: "untitled.geo" 保存在: General.SessionFileName
General.ScriptingLanguages 由 GUI 生成的脚本命令所使用的语言 默认值: "geo" 保存在: General.OptionsFileName
General.SessionFileName 会话特定信息保存到的选项文件; 启动时自动读取 默认值: ".gmshrc" 保存在: -
General.ScriptingLanguages 由 GUI 生成的脚本命令所使用的语言 默认值: "geo" 保存在: General.OptionsFileName
General.TextEditor 启动文本编辑器的系统命令 默认值: "open -t %s" 保存在: General.OptionsFileName
General.TmpFileName 几何模块使用的临时文件 默认值: ".gmsh-tmp" 保存在: General.SessionFileName
General.Version Gmsh 版本 (只读) 默认值: "4.14.0-git-697fde2e8" 保存在: -
General.WatchFilePattern 当文件可用时要合并的文件模式 默认值: "" 保存在: -
General.AbortOnError 出错时中止? (0: 否, 1: 中止网格划分, 2: 除非在交互模式下, 否则抛出异常, 3: 总是抛出异常, 4: 退出) 默认值: 0 保存在: General.OptionsFileName
General.AlphaBlending 在后处理视图中启用 alpha 混合 (透明度) 默认值: 1 保存在: General.OptionsFileName
General.Antialiasing 使用多重采样抗锯齿 (会减慢渲染速度) 默认值: 0 保存在: General.OptionsFileName
General.ArrowHeadRadius 箭头头部的相对半径 默认值: 0.12 保存在: General.OptionsFileName
General.ArrowStemLength 箭头杆的相对长度 默认值: 0.56 保存在: General.OptionsFileName
General.ArrowStemRadius 箭头杆的相对半径 默认值: 0.02 保存在: General.OptionsFileName
General.Axes 坐标轴 (0: 无, 1: 简单坐标轴, 2: 盒子, 3: 完整网格, 4: 开放网格, 5: 标尺) 默认值: 0 保存在: General.OptionsFileName
General.AxesMikado Mikado 坐标轴样式 默认值: 0 保存在: General.OptionsFileName
General.AxesAutoPosition 自动定位坐标轴 默认值: 1 保存在: General.OptionsFileName
General.AxesForceValue 强制在坐标轴上显示值 (否则使用自然坐标) 默认值: 0 保存在: General.OptionsFileName
General.AxesMaxX X 轴最大坐标 默认值: 1 保存在: General.OptionsFileName
General.AxesMaxY Y 轴最大坐标 默认值: 1 保存在: General.OptionsFileName
General.AxesMaxZ Z 轴最大坐标 默认值: 1 保存在: General.OptionsFileName
General.AxesMinX X 轴最小坐标 默认值: 0 保存在: General.OptionsFileName
General.AxesMinY Y 轴最小坐标 默认值: 0 保存在: General.OptionsFileName
General.AxesMinZ Z 轴最小坐标 默认值: 0 保存在: General.OptionsFileName
General.AxesTicsX X 轴上的刻度数 默认值: 5 保存在: General.OptionsFileName
General.AxesTicsY Y 轴上的刻度数 默认值: 5 保存在: General.OptionsFileName
General.AxesTicsZ Z 轴上的刻度数 默认值: 5 保存在: General.OptionsFileName
General.AxesValueMaxX X 轴强制最大值 默认值: 1 保存在: General.OptionsFileName
General.AxesValueMaxY Y 轴强制最大值 默认值: 1 保存在: General.OptionsFileName
General.AxesValueMaxZ Z 轴强制最大值 默认值: 1 保存在: General.OptionsFileName
General.AxesValueMinX X 轴强制最小值 默认值: 0 保存在: General.OptionsFileName
General.AxesValueMinY Y 轴强制最小值 默认值: 0 保存在: General.OptionsFileName
General.AxesValueMinZ Z 轴强制最小值 默认值: 0 保存在: General.OptionsFileName
General.BackgroundGradient 绘制背景渐变 (0: 无, 1: 垂直, 2: 水平, 3: 径向) 默认值: 1 保存在: General.OptionsFileName
General.BackgroundImage3D 在 3D 模型中 (单位 = 模型单位) 或作为 2D 背景 (单位 = 像素) 创建背景图像 默认值: 0 保存在: General.OptionsFileName
General.BackgroundImagePage 在背景图像中渲染的页面 (用于多页 PDF) 默认值: 0 保存在: General.OptionsFileName
General.BackgroundImagePositionX 背景图像的 X 位置 (对于 2D 背景: < 0: 从右窗口边缘测量; >= 1e5: 居中) 默认值: 0 保存在: General.OptionsFileName
General.BackgroundImagePositionY 背景图像的 Y 位置 (对于 2D 背景: < 0: 从下窗口边缘测量; >= 1e5: 居中) 默认值: 0 保存在: General.OptionsFileName
General.BackgroundImageWidth 背景图像的宽度 (0: 实际宽度, 如果 height = 0, 否则自然缩放; -1: 图形窗口宽度) 默认值: -1 保存在: General.OptionsFileName
General.BackgroundImageHeight 背景图像的高度 (0: 实际高度, 如果 width = 0, 否则自然缩放; -1: 图形窗口高度) 默认值: -1 保存在: General.OptionsFileName
General.BoundingBoxSize 整体边界框大小 (只读) 默认值: 1 保存在: General.OptionsFileName
General.Camera 启用相机视图模式 默认值: 0 保存在: General.OptionsFileName
General.CameraAperture 相机光圈 (度) 默认值: 40 保存在: General.OptionsFileName
General.CameraEyeSeparationRatio 立体渲染的眼间距比率 (%) 默认值: 1.5 保存在: General.OptionsFileName
General.CameraFocalLengthRatio 相机焦距比 默认值: 1 保存在: General.OptionsFileName
General.Clip0A 裁剪平面 0 的方程中的第一个系数 (‘A’ in ‘\( AX+BY+CZ+D=0 \)’) 默认值: 1 保存在: -
General.Clip0B 裁剪平面 0 的方程中的第二个系数 (‘B’ in ‘\( AX+BY+CZ+D=0 \)’) 默认值: 0 保存在: -
General.Clip0C 裁剪平面 0 的方程中的第三个系数 (‘C’ in ‘\( AX+BY+CZ+D=0 \)’) 默认值: 0 保存在: -
General.Clip0D 裁剪平面 0 的方程中的第四个系数 (‘D’ in ‘\( AX+BY+CZ+D=0 \)’) 默认值: 0 保存在: -
General.Clip1A 裁剪平面 1 的方程中的第一个系数 默认值: 0 保存在: -
General.Clip1B 裁剪平面 1 的方程中的第二个系数 默认值: 1 保存在: -
General.Clip1C 裁剪平面 1 的方程中的第三个系数 默认值: 0 保存在: -
General.Clip1D 裁剪平面 1 的方程中的第四个系数 默认值: 0 保存在: -
General.Clip2A 裁剪平面 2 的方程中的第一个系数 默认值: 0 保存在: -
General.Clip2B 裁剪平面 2 的方程中的第二个系数 默认值: 0 保存在: -
General.Clip2C 裁剪平面 2 的方程中的第三个系数 默认值: 1 保存在: -
General.Clip2D 裁剪平面 2 的方程中的第四个系数 默认值: 0 保存在: -
General.Clip3A 裁剪平面 3 的方程中的第一个系数 默认值: -1 保存在: -
General.Clip3B 裁剪平面 3 的方程中的第二个系数 默认值: 0 保存在: -
General.Clip3C 裁剪平面 3 的方程中的第三个系数 默认值: 0 保存在: -
General.Clip3D 裁剪平面 3 的方程中的第四个系数 默认值: 1 保存在: -
General.Clip4A 裁剪平面 4 的方程中的第一个系数 默认值: 0 保存在: -
General.Clip4B 裁剪平面 4 的方程中的第二个系数 默认值: -1 保存在: -
General.Clip4C 裁剪平面 4 的方程中的第三个系数 默认值: 0 保存在: -
General.Clip4D 裁剪平面 4 的方程中的第四个系数 默认值: 1 保存在: -
General.Clip5A 裁剪平面 5 的方程中的第一个系数 默认值: 0 保存在: -
General.Clip5B 裁剪平面 5 的方程中的第二个系数 默认值: 0 保存在: -
General.Clip5C 裁剪平面 5 的方程中的第三个系数 默认值: -1 保存在: -
General.Clip5D 裁剪平面 5 的方程中的第四个系数 默认值: 1 保存在: -
General.ClipFactor 近裁剪平面和远裁剪平面的距离因子 (减小该值以获得更好的 z-buffer 分辨率) 默认值: 5 保存在: -
General.ClipOnlyDrawIntersectingVolume 只绘制与裁剪平面相交的元素层 默认值: 0 保存在: General.OptionsFileName
General.ClipOnlyVolume 只裁剪体元素 默认值: 0 保存在: General.OptionsFileName
General.ClipPositionX 裁剪平面窗口左上角的水平位置 (像素) 默认值: 650 保存在: General.SessionFileName
General.ClipPositionY 裁剪平面窗口左上角的垂直位置 (像素) 默认值: 150 保存在: General.SessionFileName
General.ClipWholeElements 裁剪整个元素 默认值: 0 保存在: General.OptionsFileName
General.ColorScheme 图形的默认配色方案 (0: 浅色, 1: 默认, 2: 灰度, 3: 深色) 默认值: 1 保存在: General.SessionFileName
General.ConfirmOverwrite 覆盖文件前是否请求确认? 默认值: 1 保存在: General.OptionsFileName
General.ContextPositionX 上下文窗口左上角的水平位置 (像素) 默认值: 650 保存在: General.SessionFileName
General.ContextPositionY 上下文窗口左上角的垂直位置 (像素) 默认值: 150 保存在: General.SessionFileName
General.DetachedMenu 菜单窗口是否应与图形窗口分离? 默认值: 0 保存在: General.SessionFileName
General.DetachedProcess 在 Windows 上, 由 Gmsh 创建的进程是否应分离? 默认值: 1 保存在: General.OptionsFileName
General.DisplayBorderFactor 模型显示的边框因子 (0: 模型正好适合窗口大小) 默认值: 0.2 保存在: General.OptionsFileName
General.DoubleBuffer 使用双缓冲图形窗口 (在 Unix 上, 在没有 GLX 的远程主机上工作时应设置为 0) 默认值: 1 保存在: General.OptionsFileName
General.DrawBoundingBoxes 绘制边界框 默认值: 0 保存在: General.OptionsFileName
General.ExpertMode 启用专家模式 (以禁用所有为无经验用户准备的消息) 默认值: 0 保存在: General.OptionsFileName
General.ExtraPositionX 通用额外窗口左上角的水平位置 (像素) 默认值: 650 保存在: General.SessionFileName
General.ExtraPositionY 通用额外窗口左上角的垂直位置 (像素) 默认值: 350 保存在: General.SessionFileName
General.ExtraHeight 通用额外窗口的高度 (像素) 默认值: 100 保存在: General.SessionFileName
General.ExtraWidth 通用额外窗口的宽度 (像素) 默认值: 100 保存在: General.SessionFileName
General.FastRedraw 旋转、平移和缩放时绘制简化模型 默认值: 0 保存在: General.OptionsFileName
General.FieldPositionX 场窗口左上角的水平位置 (像素) 默认值: 650 保存在: General.SessionFileName
General.FieldPositionY 场窗口左上角的垂直位置 (像素) 默认值: 550 保存在: General.SessionFileName
General.FieldHeight 场窗口的高度 (像素) 默认值: 320 保存在: General.SessionFileName
General.FieldWidth 场窗口的宽度 (像素) 默认值: 420 保存在: General.SessionFileName
General.FileChooserPositionX 文件选择器窗口左上角的水平位置 (像素) 默认值: 200 保存在: General.SessionFileName
General.FileChooserPositionY 文件选择器窗口左上角的垂直位置 (像素) 默认值: 200 保存在: General.SessionFileName
General.FltkColorScheme FLTK 用户界面颜色主题 (0: 标准, 1: 深色) 默认值: 0 保存在: General.SessionFileName
General.FltkRefreshRate FLTK 用户界面最大刷新率, 每秒 (0: 无限制) 默认值: 5 保存在: General.OptionsFileName
General.FontSize 用户界面中的字体大小, 以像素为单位 (-1: 自动) 默认值: -1 保存在: General.OptionsFileName
General.GraphicsFontSize 图形窗口中的字体大小, 以像素为单位 默认值: 15 保存在: General.OptionsFileName
General.GraphicsFontSizeTitle 图形窗口中标题的字体大小, 以像素为单位 默认值: 18 保存在: General.OptionsFileName
General.GraphicsHeight 图形窗口的高度 (像素) 默认值: 600 保存在: General.SessionFileName
General.GraphicsPositionX 图形窗口左上角的水平位置 (像素) 默认值: 50 保存在: General.SessionFileName
General.GraphicsPositionY 图形窗口左上角的垂直位置 (像素) 默认值: 50 保存在: General.SessionFileName
General.GraphicsWidth 图形窗口的宽度 (像素) 默认值: 800 保存在: General.SessionFileName
General.HighOrderToolsPositionX 高阶工具窗口左上角的水平位置 (像素) 默认值: 650 保存在: General.SessionFileName
General.HighOrderToolsPositionY 高阶工具窗口左上角的垂直位置 (像素) 默认值: 150 保存在: General.SessionFileName
General.HighResolutionGraphics 使用高分辨率 OpenGL 图形 (例如, 适用于带 Retina 显示屏的 Mac) 默认值: 1 保存在: General.OptionsFileName
General.InitialModule 启动时启动的模块 (0: 自动, 1: 几何, 2: 网格, 3: 求解器, 4: 后处理) 默认值: 0 保存在: General.OptionsFileName
General.InputScrolling 在用户界面中启用数字输入滚动 (移动鼠标以更改数字) 默认值: 1 保存在: General.OptionsFileName
General.Light0 启用光源 0 默认值: 1 保存在: General.OptionsFileName
General.Light0X 光源 0 的 X 位置 默认值: 0.65 保存在: General.OptionsFileName
General.Light0Y 光源 0 的 Y 位置 默认值: 0.65 保存在: General.OptionsFileName
General.Light0Z 光源 0 的 Z 位置 默认值: 1 保存在: General.OptionsFileName
General.Light0W 光源 0 的 X, Y 和 Z 坐标的除数 (W=0 意味着无限远光源) 默认值: 0 保存在: General.OptionsFileName
General.Light1 启用光源 1 默认值: 0 保存在: General.OptionsFileName
General.Light1X 光源 1 的 X 位置 默认值: 0.5 保存在: General.OptionsFileName
General.Light1Y 光源 1 的 Y 位置 默认值: 0.3 保存在: General.OptionsFileName
General.Light1Z 光源 1 的 Z 位置 默认值: 1 保存在: General.OptionsFileName
General.Light1W 光源 1 的 X, Y 和 Z 坐标的除数 (W=0 意味着无限远光源) 默认值: 0 保存在: General.OptionsFileName
General.Light2 启用光源 2 默认值: 0 保存在: General.OptionsFileName
General.Light2X 光源 2 的 X 位置 默认值: 0.5 保存在: General.OptionsFileName
General.Light2Y 光源 2 的 Y 位置 默认值: 0.3 保存在: General.OptionsFileName
General.Light2Z 光源 2 的 Z 位置 默认值: 1 保存在: General.OptionsFileName
General.Light2W 光源 2 的 X, Y 和 Z 坐标的除数 (W=0 意味着无限远光源) 默认值: 0 保存在: General.OptionsFileName
General.Light3 启用光源 3 默认值: 0 保存在: General.OptionsFileName
General.Light3X 光源 3 的 X 位置 默认值: 0.5 保存在: General.OptionsFileName
General.Light3Y 光源 3 的 Y 位置 默认值: 0.3 保存在: General.OptionsFileName
General.Light3Z 光源 3 的 Z 位置 默认值: 1 保存在: General.OptionsFileName
General.Light3W 光源 3 的 X, Y 和 Z 坐标的除数 (W=0 意味着无限远光源) 默认值: 0 保存在: General.OptionsFileName
General.Light4 启用光源 4 默认值: 0 保存在: General.OptionsFileName
General.Light4X 光源 4 的 X 位置 默认值: 0.5 保存在: General.OptionsFileName
General.Light4Y 光源 4 的 Y 位置 默认值: 0.3 保存在: General.OptionsFileName
General.Light4Z 光源 4 的 Z 位置 默认值: 1 保存在: General.OptionsFileName
General.Light4W 光源 4 的 X, Y 和 Z 坐标的除数 (W=0 意味着无限远光源) 默认值: 0 保存在: General.OptionsFileName
General.Light5 启用光源 5 默认值: 0 保存在: General.OptionsFileName
General.Light5X 光源 5 的 X 位置 默认值: 0.5 保存在: General.OptionsFileName
General.Light5Y 光源 5 的 Y 位置 默认值: 0.3 保存在: General.OptionsFileName
General.Light5Z 光源 5 的 Z 位置 默认值: 1 保存在: General.OptionsFileName
General.Light5W 光源 5 的 X, Y 和 Z 坐标的除数 (W=0 意味着无限远光源) 默认值: 0 保存在: General.OptionsFileName
General.LineWidth 线的显示宽度 (像素) 默认值: 1 保存在: General.OptionsFileName
General.ManipulatorPositionX 操纵器窗口左上角的水平位置 (像素) 默认值: 650 保存在: General.SessionFileName
General.ManipulatorPositionY 操纵器窗口左上角的垂直位置 (像素) 默认值: 150 保存在: General.SessionFileName
General.MaxX 沿 X 轴的最大模型坐标 (只读) 默认值: 0 保存在: -
General.MaxY 沿 Y 轴的最大模型坐标 (只读) 默认值: 0 保存在: -
General.MaxZ 沿 Z 轴的最大模型坐标 (只读) 默认值: 0 保存在: -
General.MenuWidth 菜单树的宽度 (像素) 默认值: 200 保存在: General.SessionFileName
General.MenuHeight (分离的) 菜单树的高度 (像素) 默认值: 200 保存在: General.SessionFileName
General.MenuPositionX (分离的) 菜单树的水平位置 (像素) 默认值: 400 保存在: General.SessionFileName
General.MenuPositionY (分离的) 菜单树的垂直位置 (像素) 默认值: 400 保存在: General.SessionFileName
General.MessageFontSize 消息窗口中的字体大小, 以像素为单位 (-1: 自动) 默认值: -1 保存在: General.OptionsFileName
General.MessageHeight 消息控制台可见时的高度 (像素, 应 > 0) 默认值: 300 保存在: General.SessionFileName
General.MinX 沿 X 轴的最小模型坐标 (只读) 默认值: 0 保存在: -
General.MinY 沿 Y 轴的最小模型坐标 (只读) 默认值: 0 保存在: -
General.MinZ 沿 Z 轴的最小模型坐标 (只读) 默认值: 0 保存在: -
General.MouseHoverMeshes 在网格上启用鼠标悬停 默认值: 0 保存在: General.OptionsFileName
General.MouseSelection 启用鼠标选择 默认值: 1 保存在: General.OptionsFileName
General.MouseInvertZoom 反转鼠标滚轮缩放方向 默认值: 0 保存在: General.OptionsFileName
General.NativeFileChooser 使用原生文件选择器? 默认值: 1 保存在: General.SessionFileName
General.NonModalWindows 强制所有控制窗口在图形窗口之上 ("非模态") 默认值: 1 保存在: General.SessionFileName
General.NoPopup 在脚本中禁用交互式对话框窗口 (并使用默认值) 默认值: 0 保存在: General.OptionsFileName
General.NumThreads 当使用 OpenMP 编译时, Gmsh 使用的最大线程数 (0: 使用系统默认值, 即 OMPNUMTHREADS) 默认值: 1 保存在: General.OptionsFileName
General.OptionsPositionX 选项窗口左上角的水平位置 (像素) 默认值: 650 保存在: General.SessionFileName
General.OptionsPositionY 选项窗口左上角的垂直位置 (像素) 默认值: 150 保存在: General.SessionFileName
General.Orthographic 正交投影模式 (0: 透视投影) 默认值: 1 保存在: General.OptionsFileName
General.PluginPositionX 插件窗口左上角的水平位置 (像素) 默认值: 650 保存在: General.SessionFileName
General.PluginPositionY 插件窗口左上角的垂直位置 (像素) 默认值: 550 保存在: General.SessionFileName
General.PluginHeight 插件窗口的高度 (像素) 默认值: 320 保存在: General.SessionFileName
General.PluginWidth 插件窗口的宽度 (像素) 默认值: 420 保存在: General.SessionFileName
General.PointSize 点的显示大小 (像素) 默认值: 3 保存在: General.OptionsFileName
General.PolygonOffsetAlwaysOn 始终应用多边形偏移, 而不是尝试检测何时需要 默认值: 0 保存在: General.OptionsFileName
General.PolygonOffsetFactor 多边形偏移因子 (offset = factor * DZ + r * units) 默认值: 0.5 保存在: General.OptionsFileName
General.PolygonOffsetUnits 多边形偏移单位 (offset = factor * DZ + r * units) 默认值: 1 保存在: General.OptionsFileName
General.ProgressMeterStep 进度条的增量 (百分比) 默认值: 10 保存在: General.OptionsFileName
General.QuadricSubdivisions 用于将点或线绘制为球体或圆柱体的细分数 默认值: 6 保存在: General.OptionsFileName
General.RotationX 第一个欧拉角 (如果 Trackball=0) 默认值: 0 保存在: -
General.RotationY 第二个欧拉角 (如果 Trackball=0) 默认值: 0 保存在: -
General.RotationZ 第三个欧拉角 (如果 Trackball=0) 默认值: 0 保存在: -
General.RotationCenterGravity 围绕 (伪) 质心旋转, 而不是 (RotationCenterX, RotationCenterY, RotationCenterZ) 默认值: 1 保存在: General.OptionsFileName
General.RotationCenterX 旋转中心的 X 坐标 默认值: 0 保存在: -
General.RotationCenterY 旋转中心的 Y 坐标 默认值: 0 保存在: -
General.RotationCenterZ 旋转中心的 Z 坐标 默认值: 0 保存在: -
General.SaveOptions 当图形用户界面关闭时, 自动在 General.OptionsFileName (1) 或每个模型 (2) 中保存当前选项? 默认值: 0 保存在: General.SessionFileName
General.SaveSession 当图形用户界面关闭时, 自动在 General.SessionFileName 中保存会话特定信息? 默认值: 1 保存在: General.SessionFileName
General.ScaleX X 轴缩放因子 默认值: 1 保存在: -
General.ScaleY Y 轴缩放因子 默认值: 1 保存在: -
General.ScaleZ Z 轴缩放因子 默认值: 1 保存在: -
General.Shininess 材质光泽度 默认值: 0.4 保存在: General.OptionsFileName
General.ShininessExponent 材质光泽度指数 (介于 0 和 128 之间) 默认值: 40 保存在: General.OptionsFileName
General.ShowModuleMenu 在树状菜单中显示标准 Gmsh 菜单 默认值: 1 保存在: General.OptionsFileName
General.ShowOptionsOnStartup 启动时显示选项窗口 默认值: 0 保存在: General.OptionsFileName
General.ShowMessagesOnStartup 启动时显示消息窗口 默认值: 0 保存在: General.OptionsFileName
General.SmallAxes 显示小坐标轴 默认值: 1 保存在: General.OptionsFileName
General.SmallAxesPositionX 小坐标轴的 X 位置 (像素) (< 0: 从右窗口边缘测量; >= 1e5: 居中) 默认值: -60 保存在: General.OptionsFileName
General.SmallAxesPositionY 小坐标轴的 Y 位置 (像素) (< 0: 从下窗口边缘测量; >= 1e5: 居中) 默认值: -40 保存在: General.OptionsFileName
General.SmallAxesSize 小坐标轴的大小 (像素) 默认值: 30 保存在: General.OptionsFileName
General.StatisticsPositionX 统计窗口左上角的水平位置 (像素) 默认值: 650 保存在: General.SessionFileName
General.StatisticsPositionY 统计窗口左上角的垂直位置 (像素) 默认值: 150 保存在: General.SessionFileName
General.Stereo 使用立体渲染 默认值: 0 保存在: General.OptionsFileName
General.SystemMenuBar 在 macOS 上使用系统菜单栏? 默认值: 1 保存在: General.SessionFileName
General.Terminal 是否应在终端上打印信息 (如果可用)? 默认值: 0 保存在: General.OptionsFileName
General.Tooltips 在用户界面中显示工具提示 默认值: 1 保存在: General.OptionsFileName
General.Trackball 使用轨迹球旋转模式 默认值: 1 保存在: General.OptionsFileName
General.TrackballHyperbolicSheet 使用双曲面片在轨迹球中心外进行 z 轴旋转 默认值: 1 保存在: General.OptionsFileName
General.TrackballQuaternion0 第一个轨迹球四元数分量 (如果 General.Trackball=1) 默认值: 0 保存在: -
General.TrackballQuaternion1 第二个轨迹球四元数分量 (如果 General.Trackball=1) 默认值: 0 保存在: -
General.TrackballQuaternion2 第三个轨迹球四元数分量 (如果 General.Trackball=1) 默认值: 0 保存在: -
General.TrackballQuaternion3 第四个轨迹球四元数分量 (如果 General.Trackball=1) 默认值: 1 保存在: -
General.TranslationX X 轴平移 (模型单位) 默认值: 0 保存在: -
General.TranslationY Y 轴平移 (模型单位) 默认值: 0 保存在: -
General.TranslationZ Z 轴平移 (模型单位) 默认值: 0 保存在: -
General.VectorType 默认矢量显示类型 (用于法线等) 默认值: 4 保存在: General.OptionsFileName
General.Verbosity 在终端和消息控制台打印的信息级别 (0: 除致命错误外静默, 1: +错误, 2: +警告, 3: +直接信息, 4: +信息, 5: +状态, 99: +调试) 默认值: 5 保存在: General.OptionsFileName
General.VisibilityPositionX 可见性窗口左上角的水平位置 (像素) 默认值: 650 保存在: General.SessionFileName
General.VisibilityPositionY 可见性窗口左上角的垂直位置 (像素) 默认值: 150 保存在: General.SessionFileName
General.ZoomFactor 中键鼠标缩放加速因子 默认值: 4 保存在: General.OptionsFileName
General.Color.Background 背景颜色 默认值: {255,255,255} 保存在: General.OptionsFileName
General.Color.BackgroundGradient 背景渐变颜色 默认值: {208,215,255} 保存在: General.OptionsFileName
General.Color.Foreground 前景色 默认值: {85,85,85} 保存在: General.OptionsFileName
General.Color.Text 文本颜色 默认值: {0,0,0} 保存在: General.OptionsFileName
General.Color.Axes 坐标轴颜色 默认值: {0,0,0} 保存在: General.OptionsFileName
General.Color.SmallAxes 小坐标轴颜色 默认值: {0,0,0} 保存在: General.OptionsFileName
General.Color.AmbientLight 环境光颜色 默认值: {25,25,25} 保存在: General.OptionsFileName
General.Color.DiffuseLight 漫反射光颜色 默认值: {255,255,255} 保存在: General.OptionsFileName
General.Color.SpecularLight 镜面光颜色 默认值: {255,255,255} 保存在: General.OptionsFileName
7. 8 Gmsh 网格尺寸场
本章列出了所有 Gmsh 网格尺寸场 (参见第 1.2.2 节 [指定网格单元尺寸], 第 10 页). 场可以在脚本文件中指定 (参见第 5.3.1 节 [网格单元尺寸], 第 113 页) 或使用 API (参见第 6.5 节 [命名空间 gmsh/model/mesh/field], 第 171 页). 关于如何使用场的示例, 请参见第 2.10 节 [t10], 第 37 页.
7.1. AttractorAnisoCurve
计算到给定曲线的距离, 并在垂直于和和切向于最近曲线的方向上独立指定网格尺寸. 为了提高效率, 每条曲线都被一组采样点 (Sampling points) 替代, 实际计算的是到这些点的距离.
选项:
CurvesList 几何模型中曲线的标签 类型: list 默认值: {}
DistMax 最大距离, 在此距离之上, 从曲线处规定最大网格尺寸 类型: float 默认值: 0.5
DistMin 最小距离, 在此距离之下, 从曲线处规定最小网格尺寸 类型: float 默认值: 0.1
Sampling 每条曲线上的采样点数 类型: integer 默认值: 20
SizeMaxNormal 垂直于最近曲线方向的最大网格尺寸 类型: float 默认值: 0.5
SizeMaxTangent 切向于最近曲线方向的最大网格尺寸 类型: float 默认值: 0.5
SizeMinNormal 垂直于最近曲线方向的最小网格尺寸 类型: float 默认值: 0.05
SizeMinTangent 切向于最近曲线方向的最小网格尺寸 类型: float 默认值: 0.5
7.2. AutomaticMeshSizeField
计算一个相当自动化的网格尺寸场, 该场会考虑表面曲率和对象的接近程度.
选项:
features 启用局部特征尺寸计算 (薄通道) 类型: boolean 默认值: 1
gradation 边缘长度的最大增长率 类型: float 默认值: 1.1
hBulk 未规定处的默认尺寸 类型: float 默认值: -1
hMax 最大尺寸 类型: float 默认值: -1
hMin 最小尺寸 类型: float 默认值: -1
nPointsPerCircle 每个圆的点数 (适应表面曲率) 类型: integer 默认值: 20
nPointsPerGap 薄层中的元素层数 类型: integer 默认值: 0
p4estFileToLoad 包含尺寸场的 p4est 文件 类型: string 默认值: ""
smoothing 启用尺寸平滑 (应始终为 true) 类型: boolean 默认值: 1
7.3. Ball
在球形区域内返回 VIn, 在外部返回 VOut. 球由以下条件定义 \( \|dX\|^2 < R^2 \) 并且 \( dX = (X - XC)^2 + (Y-YC)^2 + (Z-ZC)^2 \)
如果 Thickness > 0, 网格尺寸在球周围规定厚度的层内, 在 VIn 和 VOut 之间插值.
选项:
Radius 半径 类型: float 默认值: 0
Thickness 球外部过渡层的厚度 类型: float 默认值: 0
VIn 球内部的值 类型: float 默认值: 1e+22
VOut 球外部的值 类型: float 默认值: 1e+22
XCenter 球心的 X 坐标 类型: float 默认值: 0
YCenter 球心的 Y 坐标 类型: float 默认值: 0
ZCenter 球心的 Z 坐标 类型: float 默认值: 0
7.4. BoundaryLayer
在模型中的一些曲线旁边插入一个二维边界层网格.
选项:
AnisoMax 创建边界层中网格扇区的阈值角度 类型: float 默认值: 10000000000
Beta Beta 定律的 Beta 系数 类型: float 默认值: 1.01
BetaLaw 使用 Beta 定律代替几何级数 类型: integer 默认值: 0
CurvesList 几何模型中需要边界层的曲线标签 类型: list 默认值: {}
ExcludedSurfacesList 不应构造边界层的几何模型中曲面标签 类型: list 默认值: {}
FanPointsList 为其创建扇区的几何模型中点的标签 类型: list 默认值: {}
FanPointsSizesList 每个扇区点的扇区中元素数量. 如果未提供, 则使用默认值 Mesh.BoundaryLayerFanElements 类型: list 默认值: {}
IntersectMetrics 所有曲面的相交度量 类型: integer 默认值: 0
NbLayers Beta 定律中的层数 类型: integer 默认值: 10
PointsList 边界层结束的几何模型中点的标签 类型: list 默认值: {}
Quads 在边界层中生成重组元素 类型: integer 默认值: 0
Ratio 两个连续层之间的尺寸比 类型: float 默认值: 1.1
Size 垂直于曲线的网格尺寸 类型: float 默认值: 0.1
SizeFar 远离曲线的网格尺寸 类型: float 默认值: 1
SizesList 每个点垂直于曲线的网格尺寸 (定义时覆盖 Size) 类型: list double 默认值: {}
Thickness 边界层的最大厚度 类型: float 默认值: 0.01
7.5. Box
在盒子内部返回 VIn, 在外部返回 VOut. 盒子由以下条件定义
Xmin <= x <= XMax && YMin <= y <= YMax && ZMin <= z <= ZMax
如果 Thickness > 0, 网格尺寸在盒子周围规定厚度的层内, 在 VIn 和 VOut 之间插值.
选项:
Thickness 盒子外部过渡层的厚度 类型: float 默认值: 0
VIn 盒子内部的值 类型: float 默认值: 1e+22
VOut 盒子外部的值 类型: float 默认值: 1e+22
XMax 盒子的最大 X 坐标 类型: float 默认值: 0
XMin 盒子的最小 X 坐标 类型: float 默认值: 0
YMax 盒子的最大 Y 坐标 类型: float 默认值: 0
YMin 盒子的最小 Y 坐标 类型: float 默认值: 0
ZMax 盒子的最大 Z 坐标 类型: float 默认值: 0
ZMin 盒子的最小 Z 坐标 类型: float 默认值: 0
7.6. Constant
在实体内部 (如果 IncludeBoundary 为真, 则也包括其边界) 返回 VIn, 在外部返回 VOut.
选项:
CurvesList 曲线标签 类型: list 默认值: {}
IncludeBoundary 包括实体的边界 类型: boolean 默认值: 1
PointsList 点标签 类型: list 默认值: {}
SurfacesList 曲面标签 类型: list 默认值: {}
VIn 实体内部的值 类型: float 默认值: 1e+22
VOut 实体外部的值 类型: float 默认值: 1e+22
VolumesList 体标签 类型: list 默认值: {}
7.7. Curvature
计算 Field[InField] 的曲率: F = div(norm(grad(Field[InField])))
选项:
Delta 有限差分的步长 类型: float 默认值: 0.0003464101615137755
InField 输入场标签 类型: integer 默认值: 1
7.8. Cylinder
在一个截断的圆柱体内返回 VIn, 在外部返回 VOut. 圆柱体由以下条件定义
\( \|dX\|^2 < R^2 \) 并且 \( (X-X0).A < \|A\|^2 \) \( dX = (X - X0) - ((X - X0).A)/(\|A\|^2) . A \)
选项:
Radius 半径 类型: float 默认值: 0
VIn 圆柱体内部的值 类型: float 默认值: 1e+22
VOut 圆柱体外部的值 类型: float 默认值: 1e+22
XAxis 圆柱体轴的 X 分量 类型: float 默认值: 0
XCenter 圆柱体中心的 X 坐标 类型: float 默认值: 0
YAxis 圆柱体轴的 Y 分量 类型: float 默认值: 0
YCenter 圆柱体中心的 Y 坐标 类型: float 默认值: 0
ZAxis 圆柱体轴的 Z 分量 类型: float 默认值: 1
ZCenter 圆柱体中心的 Z 坐标 类型: float 默认值: 0
7.9. Distance
计算到给定点、曲线或曲面的距离. 为了提高效率, 曲线和曲面被一组点 (根据 Sampling 采样) 替代, 实际计算的是到这些点的距离.
选项:
CurvesList 几何模型中曲线的标签 类型: list 默认值: {}
PointsList 几何模型中点的标签 类型: list 默认值: {}
Sampling 用于离散化每个曲线和曲面的线性 (即每维) 采样点数 类型: integer 默认值: 20
SurfacesList 几何模型中曲面的标签 (目前仅支持 OpenCASCADE 和离散曲面) 类型: list 默认值: {}
7.10. Extend
从给定的边界曲线 (或曲面) 向被网格划分的曲面 (或体) 内部扩展网格尺寸. 如果边界上的网格尺寸 (计算为边界单元边缘的局部平均长度) 表示为 SizeBnd, 则扩展计算如下:
\( F = f * SizeBnd + (1 - f) * SizeMax \), 如果 \( d < DistMax \) \( F = SizeMax \), 如果 \( d >= DistMax \)
其中 d 表示到边界的距离, f = ((DistMax - d) / DistMax)Power.
选项:
CurvesList 几何模型中曲线的标签 类型: list 默认值: {}
DistMax 尺寸扩展的最大距离 类型: float 默认值: 1
Power 用于插值网格尺寸的幂指数 类型: float 默认值: 1
SizeMax DistMax 之外的网格尺寸 类型: float 默认值: 1
SurfacesList 几何模型中曲面的标签 类型: list 默认值: {}
7.11. ExternalProcess
该场是实验性的 调用一个外部进程, 该进程在标准输入 (stdin) 上接收坐标三元组 (x,y,z) 作为二进制双精度数, 并应在标准输出 (stdout) 上写入场值作为二进制双精度数. NaN,NaN,NaN 作为坐标发送, 以指示进程结束.
客户端示例 (python2):
import os import struct import math import sys if sys.platform == "win32" : import msvcrt msvcrt.setmode(0, os.O_BINARY) msvcrt.setmode(1, os.O_BINARY) while(True): xyz = struct.unpack("ddd", os.read(0,24)) if math.isnan(xyz[0]): break f = 0.001 + xyz[1]*0.009 os.write(1,struct.pack("d",f))
客户端示例 (python3):
import struct import sys import math while(True): xyz = struct.unpack("ddd", sys.stdin.buffer.read(24)) if math.isnan(xyz[0]): break f = 0.001 + xyz[1]*0.009 sys.stdout.buffer.write(struct.pack("d",f)) sys.stdout.flush()
客户端示例 (c, unix):
#include <unistd.h> int main(int argc, char **argv) { double xyz[3]; while(read(STDIN_FILENO, &xyz, 3*sizeof(double)) == 3*sizeof(double)) { if (xyz[0] != xyz[0]) break; //nan double f = 0.001 + 0.009 * xyz[1]; write(STDOUT_FILENO, &f, sizeof(double)); } return 0; }
客户端示例 (c, windows):
#include <stdio.h> #include <io.h> #include <fcntl.h> int main(int argc, char **argv) { double xyz[3]; setmode(fileno(stdin),O_BINARY); setmode(fileno(stdout),O_BINARY); while(read(fileno(stdin), &xyz, 3*sizeof(double)) == 3*sizeof(double)) { if (xyz[0] != xyz[0]) break; double f = f = 0.01 + 0.09 * xyz[1]; write(fileno(stdout), &f, sizeof(double)); } }
选项:
CommandLine 要启动的命令行 类型: string 默认值: ""
7.12. Frustum
在由内半径 (R1i 和 R2i) 和外半径 (R1o 和 R2o) 以及两个端点 P1 和 P2 定义的扩展圆柱截锥体上插值网格尺寸. 点 P 的场值 F 由以下公式给出:
\( u = P1P . P1P2 / \|P1P2\| \) \( r = \| P1P - u*P1P2 \| \) \( Ri = (1 - u) * R1i + u * R2i \) \( Ro = (1 - u) * R1o + u * R2o \) \( v = (r - Ri) / (Ro - Ri) \) \( F = (1 - v) * ((1 - u) * v1i + u * v2i) + v * ((1 - u) * v1o + u * v2o) \) 其中 (u, v) 在 [0, 1] x [0, 1] 内.
选项:
InnerR1 端点 1 的截锥体内半径 类型: float 默认值: 0
InnerR2 端点 2 的截锥体内半径 类型: float 默认值: 0
InnerV1 点 1, 内半径处的网格尺寸 类型: float 默认值: 0.1
InnerV2 点 2, 内半径处的网格尺寸 类型: float 默认值: 0.1
OuterR1 端点 1 的截锥体外半径 类型: float 默认值: 1
OuterR2 端点 2 的截锥体外半径 类型: float 默认值: 1
OuterV1 点 1, 外半径处的网格尺寸 类型: float 默认值: 1
OuterV2 点 2, 外半径处的网格尺寸 类型: float 默认值: 1
X1 端点 1 的 X 坐标 类型: float 默认值: 0
X2 端点 2 的 X 坐标 类型: float 默认值: 0
Y1 端点 1 的 Y 坐标 类型: float 默认值: 0
Y2 端点 2 的 Y 坐标 类型: float 默认值: 0
Z1 端点 1 的 Z 坐标 类型: float 默认值: 1
Z2 端点 2 的 Z 坐标 类型: float 默认值: 0
7.13. Gradient
计算 Field[InField] 的有限差分梯度: \( F = (Field[InField](X + Delta/2) - Field[InField](X - Delta/2)) / Delta \)
选项:
Delta 有限差分步长 类型: float 默认值: 0.0003464101615137755
InField 输入场标签 类型: integer 默认值: 1
Kind 要评估的梯度分量: 0 表示 X, 1 表示 Y, 2 表示 Z, 3 表示范数 类型: integer 默认值: 3
7.14. IntersectAniso
根据 Alauzet 取两个各向异性场的交集.
选项:
FieldsList 场索引 类型: list 默认值: {}
7.15. Laplacian
计算 Field[InField] 的有限差分拉普拉斯算子: \( F = G(x+d,y,z) + G(x-d,y,z) + \) \( G(x,y+d,z) + G(x,y-d,z) + \) \( G(x,y,z+d) + G(x,y,z-d) - 6 * G(x,y,z) \), 其中 G = Field[InField] 且 d = Delta.
选项:
Delta 有限差分步长 类型: float 默认值: 0.0003464101615137755
InField 输入场标签 类型: integer 默认值: 1
7.16. LonLat
在地理坐标 (经度, 纬度) 中评估 Field[InField]: \( F = Field[InField](atan(y / x), asin(z / sqrt(x^2 + y^2 + z^2))) \)
选项:
FromStereo 如果 = 1, 网格位于球极坐标中: \( xi = 2Rx/(R+z) \), \( eta = 2Ry/(R+z) \) 类型: integer 默认值: 0
InField 要评估的场标签 类型: integer 默认值: 1
RadiusStereo 球极坐标的球体半径 类型: float 默认值: 6371000
7.17. MathEval
评估一个数学表达式. 表达式可以包含用于空间坐标的 x, y, z, 用于场值的 F0, F1, …, 以及数学函数.
选项:
F 要评估的数学函数. 类型: string 默认值: "F2 + Sin(z)"
7.18. MathEvalAniso
评估一个度量表达式. 表达式可以包含用于空间坐标的 x, y, z, 用于场值的 F0, F1, …, 以及数学函数.
选项:
M11 度量张量的元素 11 类型: string 默认值: "F2 + Sin(z)"
M12 度量张量的元素 12 类型: string 默认值: "F2 + Sin(z)"
M13 度量张量的元素 13 类型: string 默认值: "F2 + Sin(z)"
M22 度量张量的元素 22 类型: string 默认值: "F2 + Sin(z)"
M23 度量张量的元素 23 类型: string 默认值: "F2 + Sin(z)"
M33 度量张量的元素 33 类型: string 默认值: "F2 + Sin(z)"
7.19. Max
取一组场的最大值.
选项:
FieldsList 场索引 类型: list 默认值: {}
7.20. MaxEigenHessian
计算 Field[InField] 的 Hessian 矩阵的最大特征值, 梯度通过有限差分评估: \( F = max(eig(grad(grad(Field[InField])))) \)
选项:
Delta 用于有限差分的步长 类型: float 默认值: 0.0003464101615137755
InField 输入场标签 类型: integer 默认值: 1
7.21. Mean
返回平均值 \( F = (G(x + delta, y, z) + G(x - delta, y, z) + \) \( G(x, y + delta, z) + G(x, y - delta, z) + \) \( G(x, y, z + delta) + G(x, y, z - delta) + \) \( G(x, y, z)) / 7 \), 其中 G = Field[InField].
选项:
Delta 用于计算平均值的距离 类型: float 默认值: 0.0003464101615137755
InField 输入场标签 类型: integer 默认值: 1
7.22. Min
取一组场的最小值.
选项:
FieldsList 场索引 类型: list 默认值: {}
7.23. MinAniso
取一组可能各向异性场的交集.
选项:
FieldsList 场索引 类型: list 默认值: {}
7.24. Octree
在八叉树上预计算另一个场以加速评估.
选项:
InField 在八叉树上表示的场 ID 类型: integer 默认值: 1
7.25. Param
在参数坐标中评估 Field[InField]: F = Field[InField](FX,FY,FZ) 参见 MathEval Field 的帮助以获取有效的 FX, FY 和 FZ 表达式的描述.
选项:
FX 参数函数的 X 分量 类型: string 默认值: ""
FY 参数函数的 Y 分量 类型: string 默认值: ""
FZ 参数函数的 Z 分量 类型: string 默认值: ""
InField 输入场标签 类型: integer 默认值: 1
7.26. PostView
使用索引 ViewIndex 或标签 ViewTag (如果 ViewTag 为正) 评估后处理视图.
选项:
CropNegativeValues 返回 MAXLC 而不是负值 (此选项用于与 BackgroundMesh 选项的向后兼容性) 类型: boolean 默认值: 1
UseClosest 如果没有精确匹配, 则使用最近节点处的值 类型: boolean 默认值: 1
ViewIndex 后处理视图索引 类型: integer 默认值: 0
ViewTag 后处理视图标签 类型: integer 默认值: -1
7.27. Restrict
将一个场的应用限制在给定的几何点、曲线、曲面或体的列表上 (如果设置了 IncludeBoundary, 也包括它们的边界).
选项:
CurvesList 曲线标签 类型: list 默认值: {}
InField 输入场标签 类型: integer 默认值: 1
IncludeBoundary 包括实体的边界 类型: boolean 默认值: 1
PointsList 点标签 类型: list 默认值: {}
SurfacesList 曲面标签 类型: list 默认值: {}
VolumesList 体标签 类型: list 默认值: {}
7.28. Structured
在三维矩形结构化网格上提供的数据之间进行线性插值. 输入文件的格式是:
Ox Oy Oz Dx Dy Dz nx ny nz v(0,0,0) v(0,0,1) v(0,0,2) … v(0,1,0) v(0,1,1) v(0,1,2) … v(0,2,0) v(0,2,1) v(0,2,2) … … … … v(1,0,0) … …
其中 O 是第一个节点的坐标, D 是每个方向上节点之间的距离, n 是每个方向上的节点数, v 是每个节点上的值.
选项:
FileName 输入文件的名称 类型: path 默认值: ""
OutsideValue 网格外部的场值 (仅当 "SetOutsideValue" 选项为真时使用). 类型: float 默认值: 1e+22
SetOutsideValue 为真时使用 "OutsideValue" 选项. 如果为假, 则使用网格的最后一个值. 类型: boolean 默认值: 0
TextFormat 对于 ASCII 输入文件为真, 对于二进制文件为假 (4 字节有符号整数表示 n, 双精度浮点数表示 v, D 和 O) 类型: boolean 默认值: 0
7.29. Threshold
如果 Field[InField] <= DistMin, 返回 F = SizeMin; 如果 Field[InField] >= DistMax, 返回 F = SizeMax; 如果 DistMin < Field[InField] < DistMax, 则在 SizeMin 和 SizeMax 之间进行插值.
选项:
DistMax 在此值之后, 网格尺寸将为 SizeMax 类型: float 默认值: 10
DistMin 在此值之前, 网格尺寸将为 SizeMin 类型: float 默认值: 1
InField 计算输入值的场标签, 通常是距离 类型: integer 默认值: 0
Sigmoid 为真时使用 sigmoid 在 SizeMin 和 SizeMax 之间插值, 为假时线性插值 类型: boolean 默认值: 0
SizeMax 当值 > DistMax 时的网格尺寸 类型: float 默认值: 1
SizeMin 当值 < DistMin 时的网格尺寸 类型: float 默认值: 0.1
StopAtDistMax 为真时不在 DistMax 之外施加网格尺寸 (即, 如果 Field[InField] > DistMax, F = 一个非常大的值) 类型: boolean 默认值: 0