GMSH论文: 内置前后处理功能的三维有限元网格生成器
Table of Contents
:AUTHORS: Christophe Geuzaine¹, Jean-François Remacle² :AFFILIATION: ¹ 列日大学,电气工程与计算机科学系,Montefiore研究所,列日,比利时。² 鲁汶天主教大学,机械、材料与土木工程研究所,新鲁汶,比利时
1. 摘要
Gmsh 是一款开源的三维有限元网格生成器, 内置CAD引擎和后处理器. 它的设计目标是提供一个快速、轻量且用户友好的网格划分工具, 具有参数化输入和先进的可视化功能. 本文介绍了 Gmsh 的总体理念、主要设计选择以及其中实现的一些原创算法.
2. 关键词: 计算机辅助设计, 网格生成, 后处理, 有限元方法, 开源软件
3. 引言
当我们于1996年夏天启动 Gmsh 项目时, 我们的目标是开发一个快速、轻量且用户友好的交互式软件工具, 以便轻松创建可用于我们的三维有限元求解器 [8] 的几何体和网格, 然后以最大的灵活性可视化和导出计算结果.
当时, 还没有开源软件能同时结合CAD引擎、网格生成器和后处理器: 现有的集成工具都是昂贵的商业软件包 [41], 而免费或共享软件工具则仅限于CAD [29]、二维网格生成 [44]、三维网格生成 [53, 21, 30] 或后处理 [31].
对免费集成解决方案的需求是显而易见的, 与 Gmsh 精神相似的几个项目也大约在同一时间诞生, 其中一些至今仍在积极开发中 [39, 6]. 然而, Gmsh 的设计是独特的: 它由一个非常小的内核和四个模块 (几何、网格、求解器和后处理) 组成, 不与任何特定的计算求解器绑定, 并且从一开始就设计为既可以通过用户友好的图形界面 (GUI) 驱动, 也可以通过其自身的脚本语言驱动.
Gmsh 的第一个公开版本于1998年发布, 经过了两年时断时续的开发, 编码工作都在夜晚、周末和假期进行, 因为 Gmsh 仅仅是一个爱好, 而不是我们官方工作职责的一部分. 这个版本是仅限于 Unix 的, 以二进制形式通过互联网分发, 图形层基于 OpenGL [42], 用户界面则用 Motif [20] 编写. 经过几次更新和2000年一个短暂的仅限 Windows 的分支后, 整个用户界面在2001年初使用 FLTK [48] 进行了重写, 代码仍然以仅二进制形式发布, 适用于 Windows 和多种 Unix 操作系统. 2003年, 完整的源代码在 GNU 通用公共许可证 [17] 下发布, 并进行了修改以提供对所有主要操作系统的原生支持: Windows、MacOS 和所有 Unix/X11 变体. 2006年夏天, Gmsh 经历了一次重大重写, 导致该软件的第2版于2007年2月发布. 第2版中约50%的代码是新的: 引入了一个抽象的几何和后处理层, 网格数据结构和算法已从头重写, 图形层也已完全改造.
今天, Gmsh 在全球拥有一个由数百名用户和开发者组成的繁荣社区. 它由学术界和工业界的研究人员和工程师对一个小型、开源的、用于基于网格的数值方法的预处理和后处理解决方案的需求所驱动. 本文的目的不是成为用户指南或参考手册 (请参阅 [16]). 相反, 它是为了介绍 Gmsh 的理念和使其在免费和商业替代品中脱颖而出的原创特性.
本文的结构如下. 在第2节中, 我们概述了 Gmsh 的总体理念和设计目标, 以及为实现这些目标所做的主要技术选择. 第3、4、5和6节随后分别描述几何、网格、求解器和后处理模块. 本文在第7节以对未来发展的展望作为结论.
4. Gmsh 的设计
Gmsh 围绕四个模块构建: 几何、网格、求解器和后处理. 每个模块既可以通过GUI交互式控制, 也可以使用脚本语言控制. 所有四个模块的设计都依赖于一个简单的理念: 快速、轻量和用户友好.
- 快速: 在任何给定的时间点, 在标准个人计算机上, Gmsh 都应该能即时启动, 能够在一分钟内生成一个“大于平均水平”的网格 (与有限元社区的标准相比; 比如, 2008年的一百万个四面体), 并能够以交互式速度可视化这样的网格以及相关的后处理数据集.
- 轻量: 应用程序的内存占用应最小化, 源代码应足够小, 以便单个开发人员能够理解它. 安装或运行该软件不应依赖任何非广泛可用的第三方软件包.
- 用户友好: 图形用户界面的设计应使新用户能够在几分钟内创建简单的网格. 此外, 代码应健壮、可移植、可脚本化、可扩展并有详尽的文档——所有这些特性都有助于提供用户友好的体验.
在以下各节中, 我们描述了为实现这些时而冲突的设计目标所做的技术选择. 尽管多年来代码的主要部分已被重写, 但自1996年以来的整体初始架构和设计始终保持不变.
4.1. 2.1. 快速和轻量
为了在上述意义上实现快速和轻量, Gmsh 的内核和用户界面完全用标准 C++ [50] 编写. 内核使用 BLAS [7] 和 LAPACK 进行大部分基本线性代数运算, 内核和界面都广泛使用标准模板库 (STL) 类作为所有数据容器 (例如, vector, list, map 和 tree). 为了使算法易于理解, 我们没有过度优化其速度或内存使用, 然而 Gmsh 目前在标准个人计算机上每分钟每150MB RAM能生成约一百万个四面体, 这使其对于许多学术和工程应用来说足够强大.
图形界面是使用 FLTK [48] 和 OpenGL [42] 构建的. 使用 FLTK 而不是更大或更复杂的控件工具包, 例如 Java、TCL/TK、GTK 或 QT, 允许 Gmsh 与工具包进行静态链接. 这极大地减少了启动时间、内存占用和安装复杂性 (安装 Gmsh 只需要复制一个可执行文件), 以及构建时间——在标准个人计算机上几分钟内即可生成一个静态链接、可直接使用的可执行文件. 同样, 直接使用 OpenGL 而不是更复杂的图形库如 Inventor [49] 或 VTK [40], 使 Gmsh 保持轻量, 而不牺牲渲染性能 (Gmsh 广泛使用 OpenGL 顶点数组).
求解器和脚本接口的设计遵循相同的策略: 求解器接口使用标准的 Unix 和 TCP/IP 套接字编写, 而不是例如 Corba [54]; 脚本接口使用 Lex/Flex 和 Yacc/Bison [24] 构建, 而不是使用外部脚本语言, 例如 Python.
4.2. 2.2. 用户友好
尽管 Gmsh 可以构建为库 (然后可以与其他软件工具链接), 但它通常作为独立软件分发, 供最终用户使用. 这个独立版本既可以交互式地使用图形用户界面运行, 也可以非交互式地从命令行或通过脚本语言运行.
实现“用户友好”是关键技术选择背后的一个重要驱动因素. 我们在此详细介绍其中一些选择, 重点关注本节开头给出的期望特性列表.
4.3. 2.2.1. 健壮性和可移植性
为了实现健壮性, 即适用于尽可能广泛的输入数据范围并尽可能容忍错误的用户输入, 我们在算法的关键部分使用健壮的几何谓词 [43], 并努力在触发无法处理的异常时提供有用的错误消息.
为了在所有主要操作系统上轻松生成代码的本机版本, Gmsh 完全用标准 (C++) 编写, 并为其 GUI (FLTK) 和图形渲染 (OpenGL) 使用可移植的工具包. 将 Gmsh 在 GNU 通用公共许可证 [17] 下开源也有助于其可移植性, 因为代码已成为几个官方 Linux 发行版 (最著名的是 Debian [5]) 的一部分, 因此受益于其广泛的自动化测试基础设施. 无论是使用图形用户界面还是在批处理模式下, 相同版本的 Gmsh 现在都可以在大多数计算机上运行, 从笔记本电脑到工作站和大型HPC集群.
4.4. 2.2.2. 可脚本化
Gmsh 是可脚本化的, 以便所有输入数据都可以参数化, 并且 Gmsh 可以轻松地作为组件插入到更大的计算链中. 如上所述, Gmsh 中的脚本是使用 Lex 和 Yacc 实现的. 与由此产生的语言的紧密集成意味着提供了对内部功能的完全访问, 包括对超过500个用于微调四个模块行为的内部选项的双向访问. 例如, 脚本语言允许完全参数化所有几何实体, 在不修改源代码的情况下与外部求解器接口, 或自动化所有后处理操作, 例如创建复杂的动画或执行离屏渲染 [32].
4.5. 2.2.3. 可扩展性
我们试图方便用户和开发者修改和添加功能. 这种可扩展性对四个模块中的每一个都采取不同的形式:
- 几何: 抽象的、面向对象的几何层允许独立于底层CAD表示编写所有算法. 因此, 在源代码级别, Gmsh 通过添加对其他CAD引擎的支持而易于扩展. 目前接口了两个引擎: 原生的 Gmsh CAD引擎和 OpenCascade [38]. 添加对其他引擎的支持, 例如 Parasolid [47], 只需派生四个抽象类即可完成——见第3节. 在脚本级别, 用户可以透明地混合和匹配由不同CAD引擎内部表示的几何部件. 例如, 可以用脚本语言定义的地面模型来扩展一个 OpenCascade 的飞机模型.
- 网格: 使用抽象的几何接口, 也可以接口额外的网格划分内核. 目前,除了其自身的网格划分算法 (见第4节), Gmsh 还与 Netgen [39] 和 Tetgen [46] 接口.
- 求解器: 基于套接字的通信接口允许 Gmsh 与各种求解器接口而无需更改源代码; 当需要更精细的交互时, 也可以轻松添加定制的图形用户界面.
- 后处理: 后处理器可以通过动态加载的插件进行扩展, 以支持用户定义的操作. 这些插件以两种方式之一作用于后处理数据集 (称为视图): 要么破坏性地更改视图的内容, 要么基于当前视图创建一个或多个新视图.
所有源代码级别的扩展都可以在编译时通过基于 autoconf 的构建机制 [52] 启用或禁用, 该机制选择包含/排除代码的哪些部分.
4.6. 2.2.4. 文档和开放文件格式
文档以源代码注释和参考手册的形式提供, 其中包括几个实践教程示例和一个包含多个邮件列表和 wiki 的综合网站.
另一个有助于用户友好的重要特性是标准输入和输出文件格式的可用性. Gmsh 尽可能使用开放或事实上的标准格式, 从标准位图图形格式 (JPEG, GIF, PNG) 和矢量格式 [15] (SVG, PostScript, PDF) 到网格格式 (Ideas UNV, Nastran BDF). 结合代码的开源发布, 这极大地促进了 Gmsh 与其他计算工具的集成.
5. CAD 接口
Gmsh 从未有志于成为一个与少数成熟的、最先进的 CAD 引擎 [47, 51] 竞争的实体建模平台. 因此, 原生的 Gmsh CAD 引擎功能有限, 非常适合处理简单的学术几何体. 然而, 多年来, 越来越多的工业界人士使用 Gmsh, 这个用户社区强烈要求 Gmsh 能够对工业 CAD 模型进行网格划分.
解决这一需求的一个选项是使用交换文件, 例如 IGES (Initial Graphics Exchange Specification), VRML (Virtual Reality Markup Language) 或 STEP (STandard for the Exchange of Product model data). 然而, 使用此类交换文件格式在工程设计办公室中一直是一个麻烦的根源, 主要是因为 CAD 系统的内部数据结构通常比交换格式中的要丰富得多. 几何体的必要简化以及交换文件中未考虑到的建模公差的重要性, 导致在进行任何网格划分之前需要耗时地“修复”大多数这些交换文件.
因此, 在 Gmsh 中, 我们选择以不同的方式处理 CAD 引擎, 即通过提供对底层 CAD 模型的本机访问而无需翻译文件 (CAPRI [18] 中也使用了类似的方法). 为此, 几何模块基于一套抽象数据结构, 使我们能够表示任何实体模型的拓扑. 如第2.2.3节所述, Gmsh 可以通过为每个新引擎派生这些抽象数据结构来扩展以使用新的 CAD 引擎.
5.1. 3.1. 拓扑实体
任何三维模型都可以使用其边界表示 (BRep) 来定义: 一个体 (称为区域) 由一组曲面界定, 一个曲面由一系列曲线界定; 一条曲线由两个端点界定. 因此, 定义了四种模型实体:
模型顶点 \(G_{i}^{0}\), 是0维的拓扑实体.
模型边 \(G_{i}^{1}\), 是1维的拓扑实体.
模型面 \(G_{i}^{2}\), 是2维的拓扑实体.
模型区域 \(G_{i}^{3}\), 是3维的拓扑实体.
模型实体是拓扑实体, 即它们只处理模型中的邻接关系, 我们使用双向数据结构 [1] 来表示邻接图. 在此表示中, 维度为 (d) 的模型实体 (Gid) 包含一个向上邻接列表 \(G_{j}^{d+1}(G_{i}^{d})\), 即其所有维度为 (d+1) 的相邻实体, 以及一个维度为 (d-1) 的向下邻接列表 (Gjd-1(Gid)). 示意性地, 我们有 \[G_{i}^{0}\rightleftharpoons G_{i}^{1}\rightleftharpoons G_{i}^{2}\rightleftharpoons G_{i}^{3}\] 这种表示被称为是完备的, 因为任何模型实体都能够使用局部操作构建其任何维度的邻接列表, 即无需对模型的邻接图进行完全遍历.
5.2. 3.2. 几何描述
每个模型实体 \(G_{i}^{d}\) 都有一个形状, 一个几何. 更准确地说, 它是一个嵌入在三维空间中的 \(d\) 维流形. (请注意, 整个几何模型本身可能是非流形的: Gmsh 支持非流形特征, 如嵌入的曲线和曲面以及连接的体. 一些非流形的例子将在网格生成第4节中展示.)
模型实体的几何形状依赖于实体建模器对其底层表示. 实体建模器通常提供形状的参数化, 即一个映射 (\vec{p}∈ Rd\mapsto\vec{x}∈ R3):
- 模型顶点 \(G_{i}^{0}\) 的几何形状就是其三维位置 \(\vec{x}{i}=(x{i},y_{i},z_{i})\).
- 模型边 \(G_{i}^{1}\) 的几何形状是其底层曲线 \(\mathcal{C}{i}\) 及其参数化 \(\vec{p}(t)\in\mathcal{C}{i}\), \(T\in[t_{1},t_{2}]\).
- 模型面 \(G_{i}^{2}\) 的几何形状是其底层曲面 \(\mathcal{S}{i}\) 及其参数化 \(\vec{p}(u,v)\in\mathcal{S}{i}\). 请注意, 对于位于曲面 \(\mathcal{S}{i}\) 上的任何曲线 \(\mathcal{C}{j}\), 网格生成过程要求能够对曲面 \(\mathcal{S}{i}\) 上的任何点 \(\vec{p}(t)\in\mathcal{C}{j}\) 进行重新参数化, 即计算映射 \(u=u(t)\) 和 \(v=v(t)\). Gmsh 要么使用暴力算法计算直接映射 \(x=x(t)\), \(y=y(t)\) 和 \(z=z(t)\) 及其逆映射 \(u=u(x,y,z)\) 和 \(v=v(x,y,z)\) \(见图1\), 要么, 当底层 CAD 系统提供时, 使用模型面上点的直接重新参数化 \(即一个直接计算 (u=u(t)) 和 (v=v(t)) 的函数\).
- 与模型区域相关的几何是 \(R^{3}\).
实体建模器通常提供用于创建、操作、查询和存储三维模型的 API. 为了进行网格生成, 只需要接口这个 API 的一小部分——只需要一些查询函数.
为了获得 Gmsh 的全部功能, 对于模型边, 只需要实现五个依赖于 CAD 系统的查询函数 (见图2). 例如, 必须能够评估曲线上的映射 \(\vec{p}(t)\in\mathcal{C}\) 以及切向量 \(\vec{t}(t)=\partial_{t}\vec{p}(t)\).
对于模型面, 只需重载四个函数即可启用二维网格生成 (见图3). 请注意, 默认的二维算法不需要计算曲面参数化的导数, 因此 GFace::firstDer 函数并非严格要求 (此二维算法的描述见第4.3节).
Gmsh 中可用的其他二维算法, 以及大多数可用的二维网格生成器 (例如 bamg [19] 或 blsurf [23]), 都使用参数化的导数.
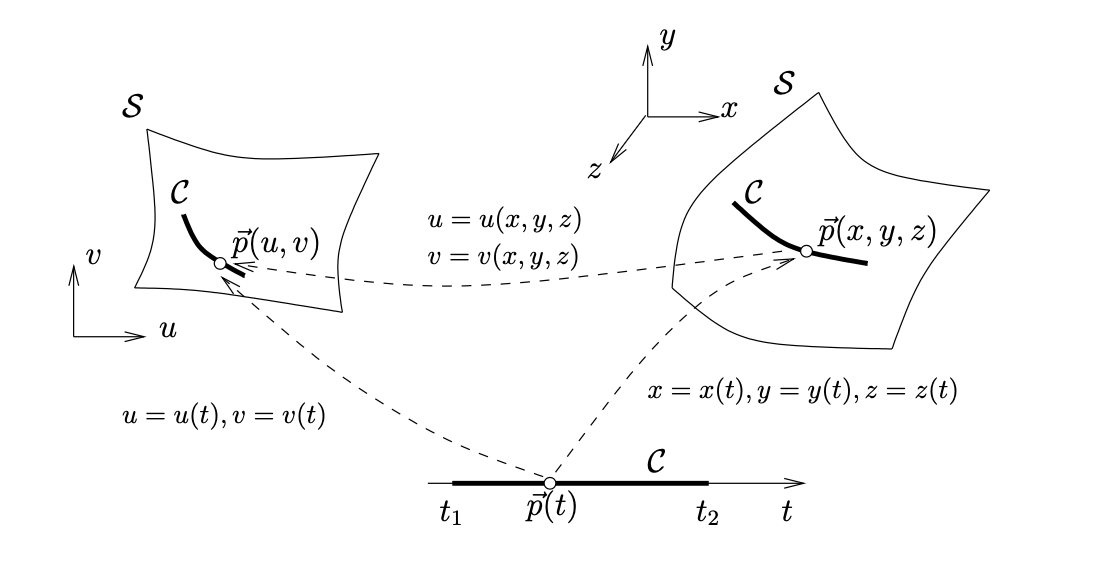
Figure 1: 点p位于曲线C上, 曲线C本身嵌入在曲面S中.
class GEdge : public GEntity{ // bi-directional data structure GVertex *v1, *v2; std::list<GFace*> faces; public: // pure virtual functions that have to be overloaded for every // solid modeler virtual std::pair<double> parRange() = 0; virtual Point3 point(double t) = 0; virtual Vector3 firstDer(double t) = 0; virtual Point2 reparam(GFace *f, double t, int dir) = 0; virtual bool isSeam(GFace *f) = 0; // other functions of the class are non pure virtual // ... };
class GFace : public GEntity{ // bi-directional data structure GRegion *r1, *r2; std::list<GEdge*> edges; public: // pure virtual functions that have to be overloaded for every // solid modeler virtual std::pair<double> parRange(int dir) const = 0; virtual Point3 point(double u, double v) const = 0; virtual std::pair<Vector3> firstDer(double u, double v) const = 0; // other functions of the class are non pure virtual virtual double curvature(double u, double v) const; // ... };
5.3. 3.3. 实体模型
一个 Gmsh 模型只是简单地构建为一个模型实体列表, 其中每个实体可能具有不同的底层几何. 事实上, 如前所述, 多个 CAD 模型可以共存于同一个 Gmsh 模型中. 在实践中, 混合来自不同 CAD 引擎的部件可能非常有趣: 例如, 用一个 CAD 建模器设计的复杂、不可参数化的部件 (比如, 一个完整的飞机模型) 可以用 Gmsh 原生建模器的脚本语言编写的可参数化部件来扩展 (比如, 一个希望优化其设计的雷达天线). 然后, 整个模型可以在没有任何 CAD 转换的情况下进行离散化和优化.
6. Gmsh 中的网格生成
为了描述网格生成过程, 让我们考虑图4中展示的一个螺旋桨的 CAD 模型. 该模型是使用 OpenCascade 实体建模器创建的, 并以其原生格式 (brep) 加载到 Gmsh 中. 该模型包含101个模型顶点, 170条模型边, 76个模型面和一个模型区域.

Figure 2: 螺旋桨的CAD模型 (左) 及其体网格 (右)
6.1. 4.1. 网格尺寸场和质量度量
让我们将网格尺寸场 \(\delta(x,y,z)\) 定义为一个函数, 该函数在域的每个点上定义该点处元素的目标尺寸. 目前在 Gmsh 中定义此类网格尺寸场的方法有:
在模型顶点处指定网格尺寸, 并在模型边上进行线性插值;
在模型边上指定网格分级 (几何级数, …);
在域的另一个网格 (背景网格) 上定义网格尺寸;
网格尺寸适应模型实体的曲率主值.
这些尺寸场随后可以被函数作用, 这些函数可能依赖于, 例如, 到模型实体的距离或用户指定的解析函数; 当提供多个尺寸场时, Gmsh 使用所有场的最小值. 由于这个机制, Gmsh 允许在给定模型实体上定义的网格尺寸场扩展到更高维的实体中. 例如, 使用距离函数, 基于模型边曲率的细化可以扩展到任何与其相邻的曲面上.
现在让我们考虑网格的一条边 (e). 我们将边相对于尺寸场 \(\delta\) 的无量纲长度定义为 \[l_{e}=\int_{e}\frac{1}{\delta(x,y,z)}dl. \quad(1)\] 网格生成过程的目标是双重的:
生成一个网格, 其中每条网格边 \(e\) 的尺寸接近于 \(l_{e}=1\).
生成一个网格, 其中每个元素 (K) 的形状良好.
换句话说, 网格生成过程的目标是能够构建一个符合网格尺寸场的高质量网格.
为了快速评估网格与规定的网格尺寸场之间的匹配程度, 我们定义了一个效率指数 \(\tau\) [13] 为 \[\tau=\exp\left(\frac{1}{n_e}\sum_{e=1}^{n_e}\tau_{e}\right) \quad(2)\] 其中 \(\tau_{e}=l_{e}-1\) \(如果 (le<1)) 以及 (τe=\frac{1}{le}-1) (如果 (le≥1)). 效率指数的范围在 (τ∈[0,1]) 之间, 并且应尽可能接近 (τ=1).
为了测量元素的质量, 文献中有各种元素形状度量 [33, 27]. 在这里, 我们选择一个基于元素半径比的度量, 即内切圆与外接圆的半径之比. 如果 (K) 是一个三角形, 我们有以下公式 \[\gamma_{K}=4\frac{\sin\hat{a}\sin\hat{b}\sin\hat{c}}{\sin\hat{a}+\sin\hat{b}+\sin\hat{c}}\] 其中 (\hat{a}, \hat{b}) 和 (\hat{c}) 是三角形的三个内角. 根据这个定义, 等边三角形的 (γK=1), 退化 (零面积) 三角形的 (γK=0). 对于一个四面体, 我们有以下公式: \[\gamma_{K}=\frac{6\sqrt{6}V_{K}}{\left(\sum_{i=1}^{4}a(f_{i})\right) \left(\sum_{j=1}^{6}l(e_{j})\right)}\] 其中 \(V_{K}\) 是 K 的体积, \(a(f_{i})\) 是 K 的第 \(i\) 个面的面积, \(l(e_{j})\) 是 K 的第 \(j\) 条边的有量纲长度. 这个质量度量位于区间 [0, 1] 内, \(\gamma_{K}=0\) 的元素是裂片 (sliver) (零体积).
6.2. 4.2. 一维网格生成
让我们考虑曲线 C 上的一个点 \(\vec{p}(t)\), \(t\in[t_{1},t_{2}]\). 曲线的细分数 N 是其无量纲长度: \[\int_{t_{1}}^{t_{2}}\frac{1}{\delta(x,y,z)}||\partial_{t}\vec{p}(t)||dt=N. \quad(3)\] 曲线上的 N+1 个网格点位于坐标 \({T_{0},...,T_{N}}\), 其中 \(T_{i}\) 通过以下规则计算: \[\int_{t_{1}}^{T_{i}}\frac{1}{\delta(x,y,z)}||\partial_{t}\vec{p}(t)||dt=i. \quad(4)\] 通过这种选择, 曲线的每个细分段的无量纲尺寸都恰好为1, 并且一维网格精确满足尺寸场 \(\delta\). 在 Gmsh 中, (4) 是用递归数值积分规则来评估的.
6.3. 4.3. 二维网格生成
由 CAD 系统设计的曲面形状通常由参数化曲面定义, 例如 NURBS [34]. 让我们考虑一个模型面 \(G_{i}^{2}\) 及其底层几何, 在这种情况下是一个曲面 \(\mathcal{S}\in R^{3}\) 及其参数化 \(\vec{p}(u,v)\in\mathcal{S}\), 其中参数 (u, v) 的定义域由一系列边界曲线定义. 图5给出了这样一个曲面的一个例子, 它显示了螺旋桨76个模型面之一在参数空间 (左) 和真实空间 (右) 中的情况.
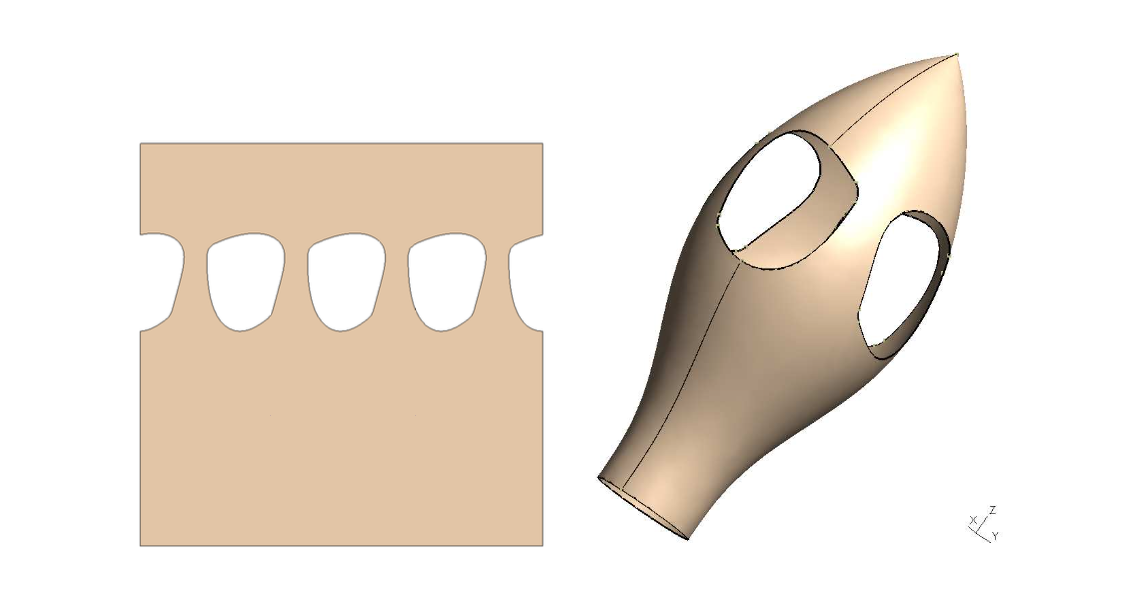
Figure 3: 模型面在参数空间 (左) 和真实空间 (右) 中的几何形状. 面上存在两条接缝边. 顶部的模型边退化为一个点.
曲面S的三个在CAD描述中常见的特征, 使其网格划分不那么简单:
S 是周期性的. 为了正确定义其闭包, 模型面的拓扑被修改. 一条接缝在模型面的闭包中出现两次. 这两次出现被参数空间中的一个周期隔开.
S 是修剪过的: 它包含四个孔, 其中一个孔被接缝穿过.
S 的一个模型边是退化的. 这是为了处理曲面参数化中的一个奇点. 这种退化存在于许多形状中: 球体、圆锥体和其他旋转曲面.
在曲面上生成有限元网格的技术有两种:
直接在真实三维空间中生成曲面网格的技术;
在参数空间中生成曲面网格的技术.
大多数直接在真实三维空间中工作的算法通过修改现有的几何网格来工作 [11]. 例如, 此类算法已被用于从STL (stereolithography) 数据文件 [2] 或医学成像 [57] 构建网格. 这些算法的主要优点是不需要与实体建模器接口. 此类算法的主要缺点是它们的相对缺乏健壮性, 因为在真实空间中检查网格修改的有效性需要启发式方法, 例如法线之间角度的最大容差.
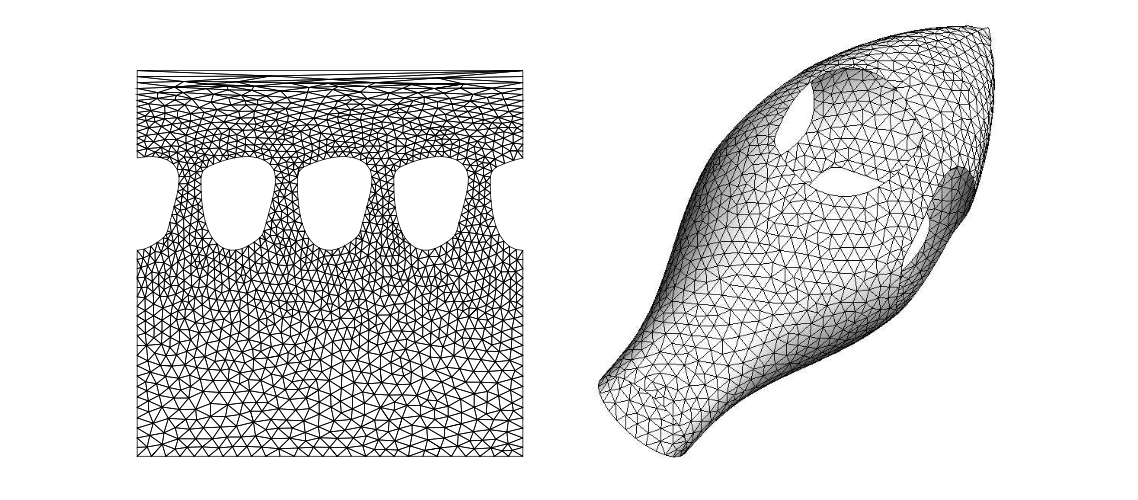
Figure 4: 模型面的网格在参数空间 (左) 和真实空间 (右) 中的绘制.
第二种选择只有在曲面的参数化可用时才能应用. 如果是这样, 在参数空间中进行网格划分通常是有利的, 因为所有的网格划分过程都可以在参数平面上应用. 这使得网格操作符高度健壮: 在平面上构建一个有效的三角剖分总是可能的, 并且可以保证元素不重叠. 然而, 并非所有曲面都总是有保持角度和长度的参数化. 因此, 只有允许在平面上构建各向异性网格的二维算法才能被认为是进行曲面网格划分的良好候选者. 图6展示了图5模型面的曲面网格, 分别在参数空间和真实空间中. 真实空间中的网格是各向同性和均匀的, 而参数空间中的网格是高度各向异性和非均匀的.
为了解决这个问题, George和Borouchaki [12] 提出了使用源自曲面第一基本形式的度量. 度量场是一个二阶张量场, 在参数空间的任何一点上, 它都具有 (2×2) 矩阵的形式. 该度量用于在参数空间中定义角度和距离. 通过他们的 Delaunay 方法, “空圆”属性有效地变成了“空椭圆”属性. Cuilliere 在 [4] 中提出了一种等效的“基于度量”的前沿推进曲面网格生成算法. Yamada 等人 [45] 设计了一种更奇特的基于椭圆堆积的度量方法, 并最近被 Lo 和 Wang 在 [28] 中使用.
除了类似于 [12] 的 Delaunay 实现和受 [35] 启发的阵面-Delaunay 网格技术外, Gmsh 还提供了一种基于局部网格修改概念的原创曲面网格策略 [25, 26, 36]. 与其他基于 Delaunay 准则的方法相比, 新方法的主要优点是它不需要计算参数化的导数. 因此, 即使参数化是奇异的, 新方法仍然保持健壮.

Figure 5: 局部网格修改的图示.
该算法的工作方式如下. 首先, 使用分治策略 [9] 在参数空间中构建一个包含面边界曲线上所有网格点的初始网格. 然后, 使用交换操作 [56] 恢复一维离散化的所有边. 最后, 应用局部网格修改:
每条太长的边都被分割;
每条太短的边都使用边塌陷操作移除;
通过交换可以获得更好配置的边被交换;
顶点被优化地重新定位.
更准确地说, 以下是这四种局部网格修改程序在 Gmsh 中的应用方式:
边分割: 当一条边的无量纲长度大于 \(l_{e}>1.4\) 时, 认为它太长. 分割后, 两条新边的最小尺寸将为0.7. 为了收敛到一个稳定的配置, 尺寸为 \(l_{e}=0.7\) 的边不应被视为短边.
边塌陷: 当一条边的无量纲长度小于 \(l_{e}<0.7\) 时, 认为它太短. 如果塌陷后剩余的任何一个三角形在参数空间中发生翻转, 则不能塌陷该边.
边交换: 如果 \(min(\gamma_{e_{1}},\gamma_{e_{2}}\)
它被分类在模型边上;
两个相邻的三角形 \(e_{1}\) 和 \(e_{2}\) 在参数空间中形成一个凹四边形;
三角形法线之间的角度大于一个阈值, 通常是30度.
顶点重定位: 每个顶点在其周围所有三角形组成的腔内进行优化移动. 选择最佳位置以最大化最差的元素质量 [10].
对于这些局部网格修改程序中的每一个, 进行网格修改的机会在真实空间, 即(x, y, z)中进行评估, 而网格修改的有效性则在参数空间(u, v)中进行评估. 因此, Gmsh 网格生成器总是保留任何网格顶点的真实坐标和参数坐标. 为确保健壮性, 所有基本的几何谓词都使用健壮的算法 [43].
在实践中, 该算法在大约6-8次迭代后收敛, 并在不计算映射导数的情况下在参数空间中生成各向异性网格. 让我们用一个例子来说明该算法. 我们使用解析尺寸场对图6的模型面进行了网格划分 \[\delta(x,y,z)=\delta_{0}[1+\cos(\pi(x+y-z)/L)]+\epsilon\] 其中 L 是域的特征尺寸, (ε≪δ0
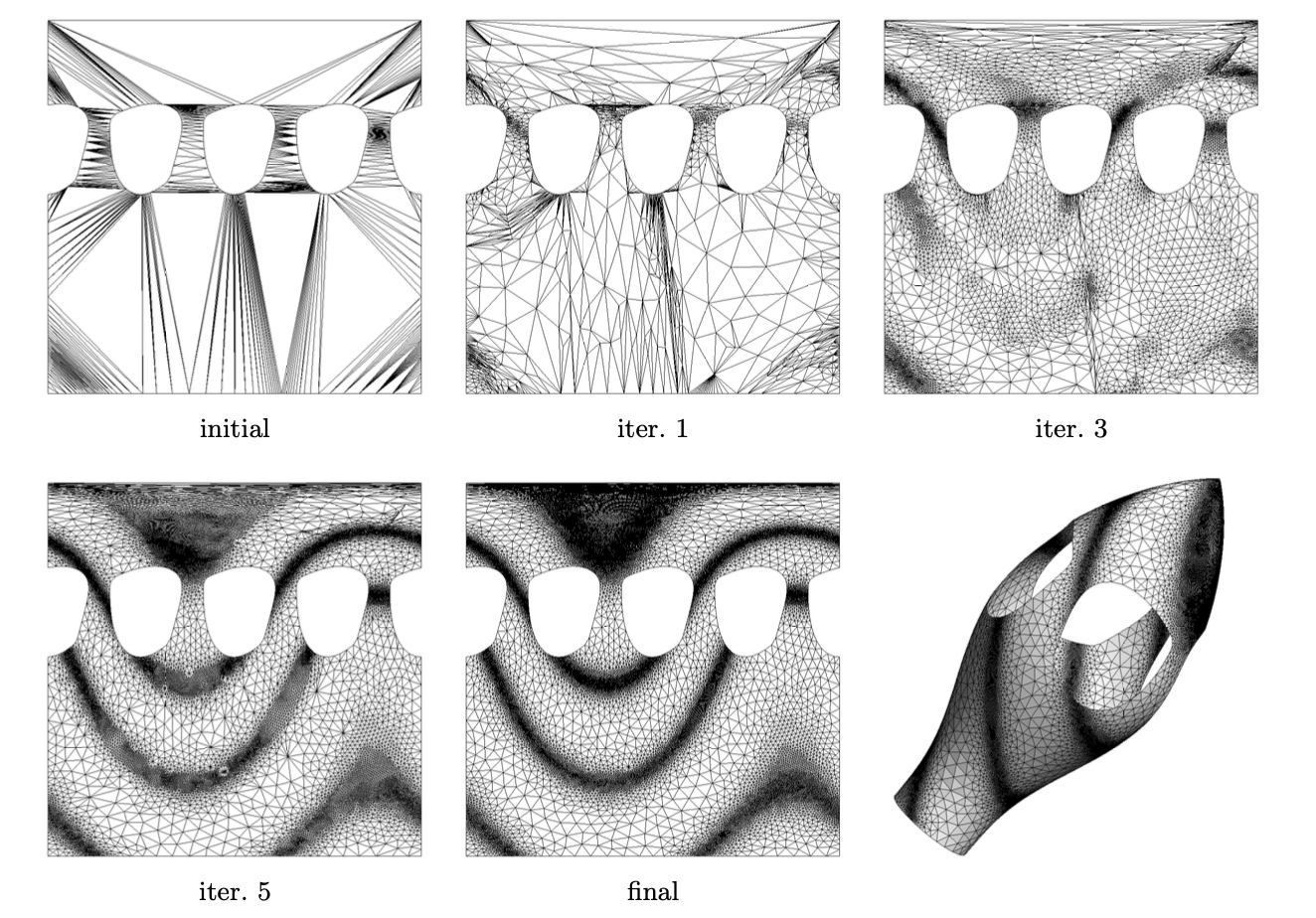
Figure 6: 基于局部网格修改的曲面网格算法图示. 图像对应于包含边界顶点的初始网格, 以及经过1、3、5和8次迭代后的网格. 在第8次迭代时, 算法已收敛. 尺寸场效率 (τ=0.89) 可被认为是优秀的: 90%的单元的半径比 (γK) 大于0.9.
6.4. 4.4. 三维网格生成
一旦曲面三角剖分可用, 自动网格生成过程通常不需要与 CAD 系统接口. 实际上, Gmsh 除了自己的 Delaunay 细化算法外, 还接口了几个开源的三维四面体网格生成内核 [39, 46]. 这些算法是标准的 [14, 39], 在此不再解释. 我们将重点关注另外两个问题:
Gmsh 接口多个网格生成算法的方式;
Gmsh 优化三维网格质量的方式. (第三个问题涉及 Gmsh 如何处理混合结构/非结构网格——这在第4.6节中讨论.)
6.4.1. 4.4.1. 网格算法接口
Gmsh 能够处理大多数标准的有限元形状: 线、三角形、四边形、四面体、六面体、棱柱和金字塔. 内部网格数据结构旨在最小化内存占用而不损害灵活性: 除了一个整数标签和一个分区/可视化索引外, 任何元素只保存其有序的顶点列表. 通过这种简单的设计, Gmsh 每GB内存可以加载约1200万个四面体 (每个四面体28字节, 每个网格顶点44字节), 包括图形表示, 即 OpenGL 顶点数组 [42].
当使用“内部”网格划分例程时, Gmsh (在面向对象的意义上) 派生出专门为每个网格划分算法定制的丰富数据结构. 这些派生结构仅包含必要的额外信息: 用于参数化二维网格划分算法的顶点的参数坐标, 用于三维 Delaunay 算法的四面体的邻居等. 通过这种方法, 四面体的占用空间例如扩展到84字节, 而 Gmsh 中实现的、使用经典 Bowyer-Watson 算法 [55] 的三维 Delaunay 算法, 每GB内存能够构建约700万个四面体 (包括 CAD 引擎数据结构等开销).
当调用第三方网格生成器时, Gmsh 当然需要分配该特定软件所需的适当结构. 但值得庆幸的是, 在将数据从第三方算法传输到 Gmsh 时, 只需要分配最小的内部数据结构 (即在上述三维情况下每个四面体28字节). 这极大地减少了接口外部算法所产生的开销.
6.4.2. 4.4.2. 四面体网格改进
四面体网格改进通常是生成适用于基于网格的数值方法的三维网格所必需的 [10]. 不幸的是, 网格优化过程有很多“黑魔法”的成分: 即使构建网格优化过程所需的要素是众所周知的 (主要是交换和平滑), 也没有已知的“最佳配方”, 即没有已知的组合这些平滑和交换操作符的最佳方式.
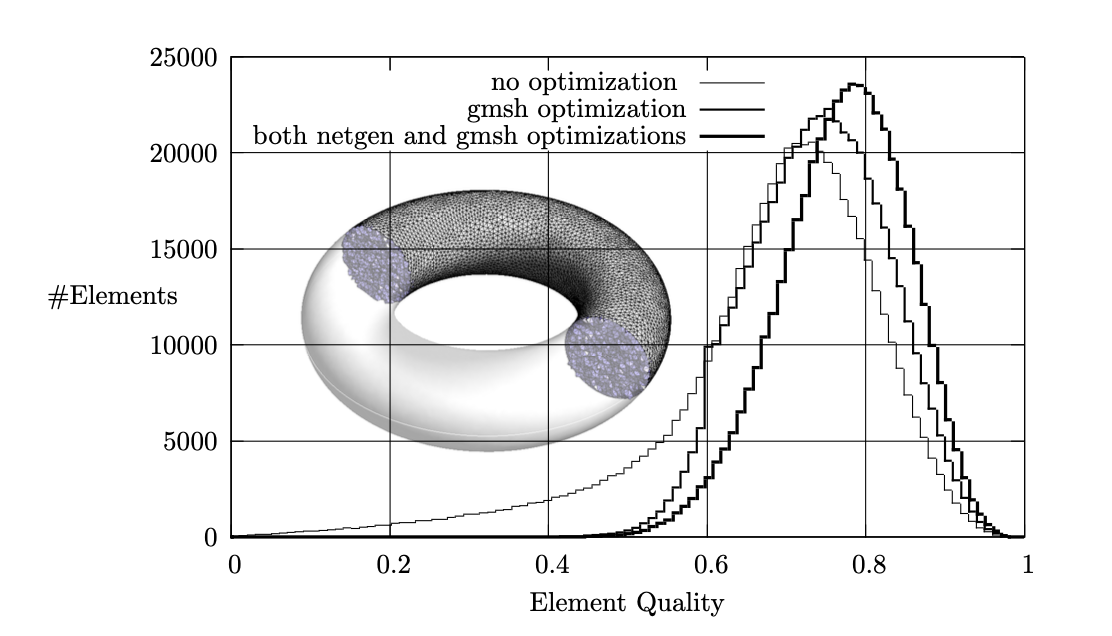
Figure 7: 一个包含约60万个四面体的环形域网格中 (γK) 的分布.
Gmsh 实现了自己的网格优化程序, 通过边和面交换以及顶点重定位来提高四面体网格质量, 并且还接口了第三方网格优化器, 特别是来自 Netgen [39] 的开源优化器. 有趣的是, 依次应用优化例程比单独应用网格优化器能够产生更好的网格. 图9显示了一个包含约60万个四面体的环形域网格上的单元质量分布 (该网格使用“内部”三维Delaunay算法在约30秒内生成). 未优化的网格包含相当多形状不佳的单元: 超过5000个单元的纵横比 (γK) 低于0.2, 形状最差的单元的纵横比为 (10-3). 经过一次 Gmsh 网格优化器处理后 (耗时约12秒), 所有裂片都消失了, 最差单元的纵横比为0.32. 单元质量的分布得到增强, 分布明显右移. 在 Gmsh 优化器之后应用 Netgen 优化器, 可以观察到额外的改进: 最差的单元质量现在是0.41, 并且发生了另一次右移. 然而, Netgen 优化器的应用也显著减少了网格中的单元数量, 并且这第二次优化过程耗时超过200秒——大约是 Gmsh 优化器的15倍. 将网格以 Netgen 格式传输也使内存使用量增加了一倍.
6.5. 4.5. 示例
本节的目标之一是展示 Gmsh 能够构建可供有限元社区使用的网格. 下面展示的各种示例都可以从 Gmsh 网站下载. 它们来自不同的来源: 原生的 Gmsh CAD 模型、在网络上找到的 CAD 模型, 或由工业和学术合作伙伴提出的 CAD 模型. 考虑的格式有 IGES, STEP, BREP 和 Gmsh. 使用了各种尺寸场, 均匀或非均匀. 提供了二维和三维的统计数据.
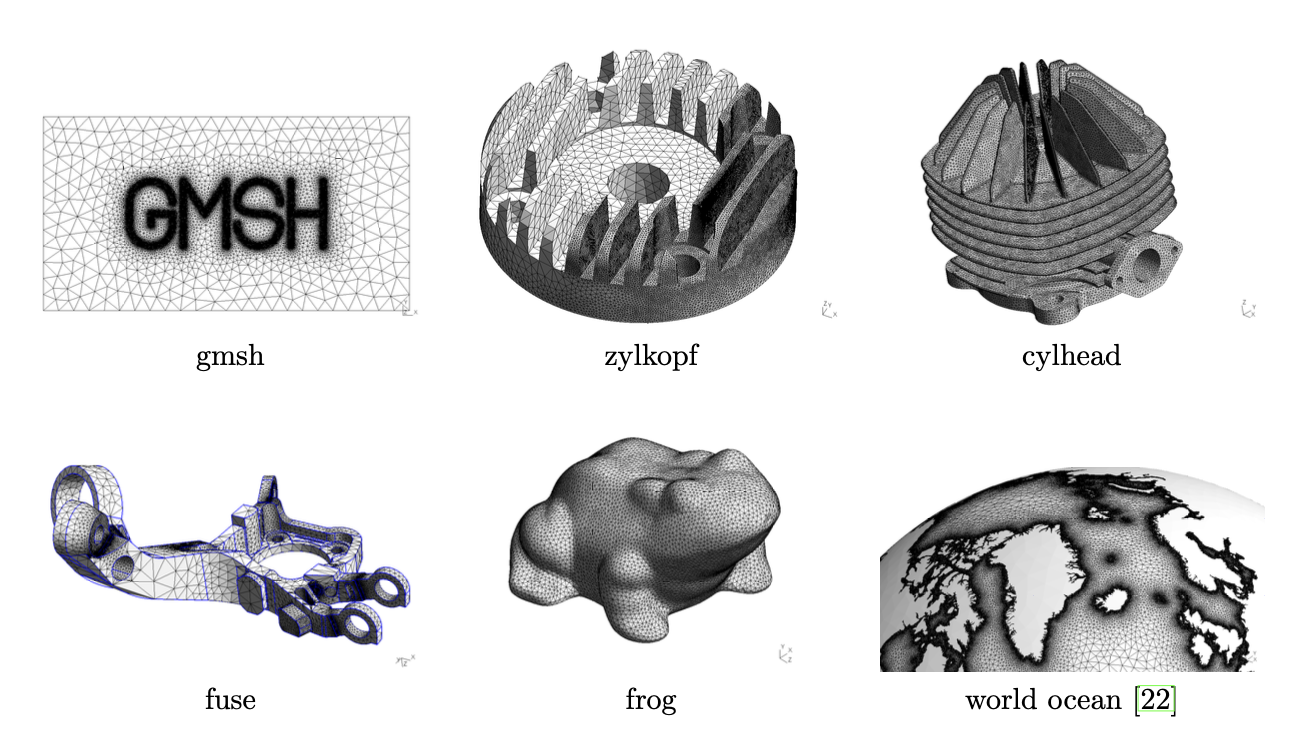
Figure 8: 一些曲面网格的图像.
表 I 展示了 Gmsh 二维测试套件中使用的一些模型 (见图10) 的详细信息. 网格尺寸场以多种方式定义: 解析、均匀、由距离函数驱动的尺寸场 (吸引子)、边界层、与曲面曲率相关的尺寸场, 或使用在模型顶点上定义的尺寸进行插值的尺寸场. 表 II 给出了使用第4.3节中介绍的曲面网格算法生成的二维网格的统计数据. 在平面和均匀网格的情况下, 该算法比 Gmsh 中实现的二维各向异性 Delaunay 网格生成器慢约三倍. 然而, 当涉及多个尺寸场和/或当曲面非常复杂时, 这种新方法在 CPU 时间方面变得具有竞争力, 并且比各向异性 Delaunay 网格生成器更健壮. 尽管网格生成算法的性能和健壮性高度依赖于其实现, 我们相信这表明第4.3节中提出的新算法是经典 Frontal 或 Delaunay 方法的可行替代方案.
表 III 给出了一些三维网格的统计数据. 第一个例子可以作为参考: 它是一个单位立方体, 均匀地划分为约一百万个四面体. 一些例子具有复杂的网格尺寸场 (linkrods 或 frogadapt). 有一个几何形状中有小特征 (block). 有些有多个体积 (media 或 senzor). 像 linkrods 或 frogadapt 那样复杂的网格尺寸场使网格生成过程慢了约20%. 这种开销主要归因于网格尺寸场的评估. 具有强烈尺寸变化或小几何特征的网格需要更多的优化. 第4.4.1节中提到的性能数据即使对于具有大量模型区域的模型也成立: 名为“media”的模型, 在原生 Gmsh CAD 格式中创建, 涉及超过1000个模型区域, 并使用三维 Delaunay 算法在不到一分钟内完成网格划分. 所有计时都在主频为2.0 GHz 的标准 MacBook Pro 上测量.
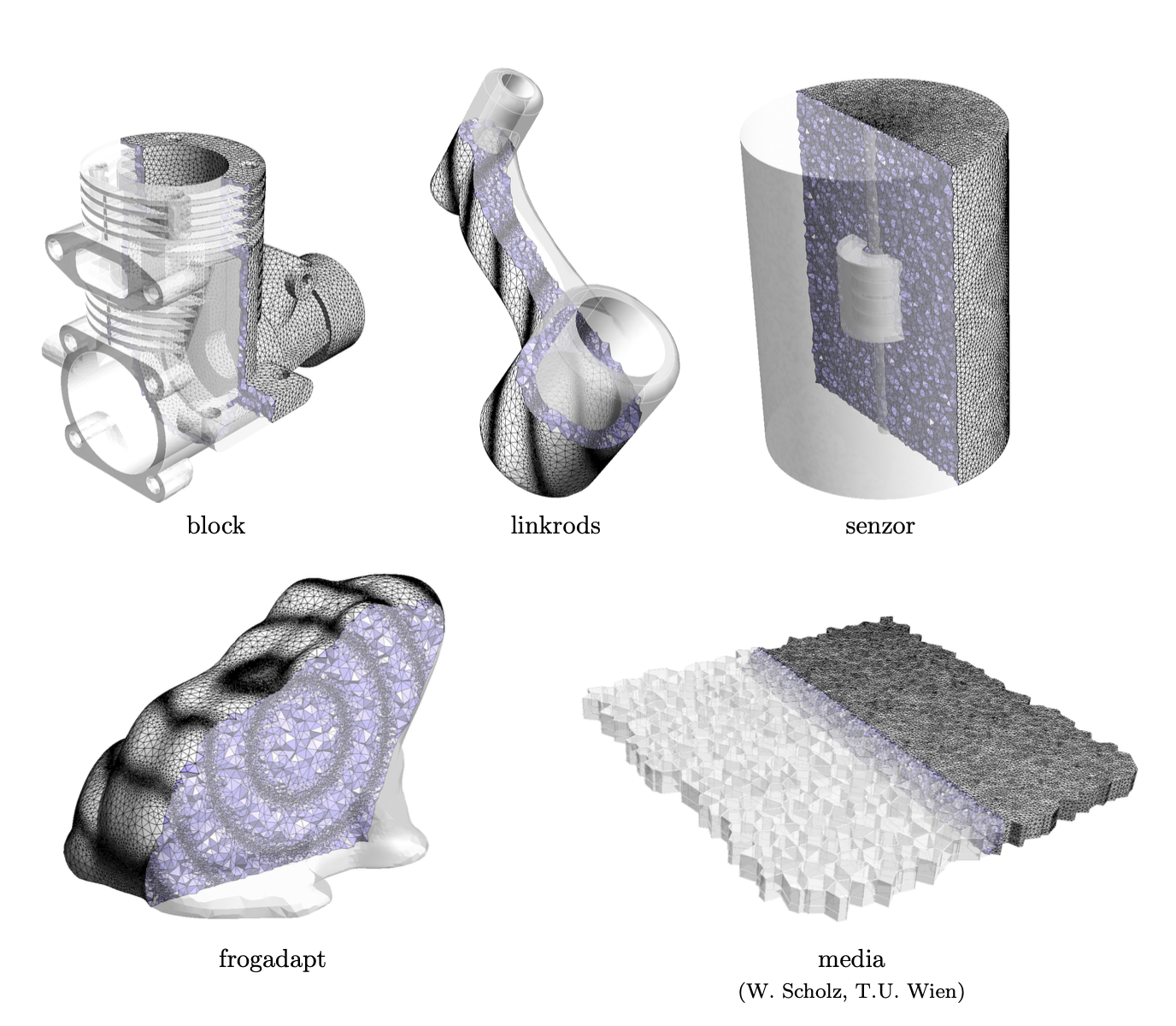
Figure 9: 一些体网格的图像.
Table I. 所考虑模型的统计数据: (n_{R}), (n_{F}), (n_{E}) 和 (n_{V}) 分别是模型中模型区域、模型面、模型边和模型顶点的数量. (\delta) 是尺寸场.
,类型, (n_{R}), (n_{F}), (n_{E}), (n_{V}), (\delta)
"cube", "GMSH", "1", "6", "12", "8", "uniform"
"gmsh", "GMSH", "0", "1", "35", "23", "attractor"
"frog", "IGES", "1", "475", "950", "477", "uniform"
"frogadapt", "IGES", "1", "475", "950", "477", "analytic"
"linkrods", "STEP", "1", "37", "108", "74", "analytic"
"zylkopf cylhead", "STEP BREP", "1 1", "137 1054", "404 2485", "270 1445", "at vertices uniform"
"fuse", "STEP", "1", "249", "723", "476", "curvature"
"block", "STEP", "1", "533", "1586", "1048", "uniform"
"senzor", "GMSH", "8", "90", "200", "146", "at vertices"
"world ocean", "GMSH", "0", "1", "4245", "145291", "boundary layer"
"media", "GMSH", "1274", "8398", "5779", "3894", "uniform"
Table II. 曲面网格生成统计. 这里, (n_p) 和 (n_e) 分别是曲面网格中的点数和三角形数, (\gamma_{K}>0.9) 表示质量度量大于0.9的三角形的百分比, (min \gamma_K) 是曲面网格中最差的元素质量, (avg \gamma_K) 是平均元素质量. (l_{\sqrt{2}}) 表示无量纲长度在 (1/\sqrt{2}
#+BEGIN_SRC text
Table III. 体网格生成统计. 这里, (n_p) 和 (n_e) 分别是体网格中的点数和四面体数, (min \gamma_K) 是体网格中最差的元素质量, (avg \gamma_K) 是平均元素质量. 最后两列给出了网格生成和网格优化的计时.
, (n_p), (n_e), (min \gamma_K), (avg \gamma_K), CPU (mesh), CPU (opti)
"cube", "195,671", "1,098,530", "0.235", "0.717", "49 sec.", "36 s"
"linkrods", "341,297", "1,836,634", "0.347", "0.756", "111 s", "117s"
"block", "48,897", "221,090", "0.012", "0.660", "12 s", "14s"
"senzor", "143,799", "805,392", "0.222", "0.765", "35 s", "27 s"
"frogadapt", "403,947", "2,381,969", "0.172", "0.691", "116 s", "180 s"
"media", "164,517", "890,756", "0.071", "0.696", "55 s", "31 s"
6.6. 4.6. 混合网格
除了非结构化网格, Gmsh 还能够在一维、二维和三维中生成简单的结构化网格, 并允许将这些网格与非结构化网格耦合. 结构化技术包括跨限和椭圆网格以及各种扫掠技术. 例如, 要从一组源曲面构建边界层网格 (见图12), Gmsh
通过从所有源曲面扫掠零高度体积来创建边界层的拓扑. (除了边界层体积, 这还创建了一组新的边界层点、曲线和曲面. 这些新的点、曲线和曲面只有在网格划分过程中才会获得具体的表示.)
对源曲面进行网格划分, 并计算网格顶点的 (唯一) 法线;
沿着法线扫掠边界层点, 并重新划分连接到这些点的所有非边界层曲线, 然后通过沿法线扫掠来划分边界层曲线;
划分非源曲面, 然后是边界层曲面 (同样通过沿法线扫掠), 最后是体积.
一旦所有结构化部分都被划分网格, 剩余部分将使用非结构化算法进行网格划分, 从而产生协调的混合网格. 为了使最终网格是协调的, 结构化算法在需要时会将六面体、棱柱或金字塔分割成单纯形.

Figure 10: 一些混合体网格的图像.
7. 求解器接口
当 Gmsh 作为库构建时, 有限元求解器可以直接与其链接, 并使用 Gmsh API 加载几何、生成网格或后处理数据. 这种方法非常强大, 但需要在求解器开发者方面进行大量的编程投入.
遵循我们“用户友好”的设计目标, Gmsh 提供了一种侵入性较小但仍然强大的替代方案: 外部求解器可以通过 Unix 和 TCP/IP 套接字与 Gmsh 接口. 这允许从后处理模块内部 (见第6节) 启动外部计算, 并直接收集和处理结果, 而求解器方面只需要进行最少的更改. 脚本化接口允许通过编辑文本文件中的选项来添加对新求解器的支持, 因此可以不加改变地直接使用标准的独立版 Gmsh.
与 Gmsh 接口的默认求解器是 GetDP [8] (见图13), 并且还提供了用多种语言 (C, C++, Perl 和 Python) 编写的求解器的模板.
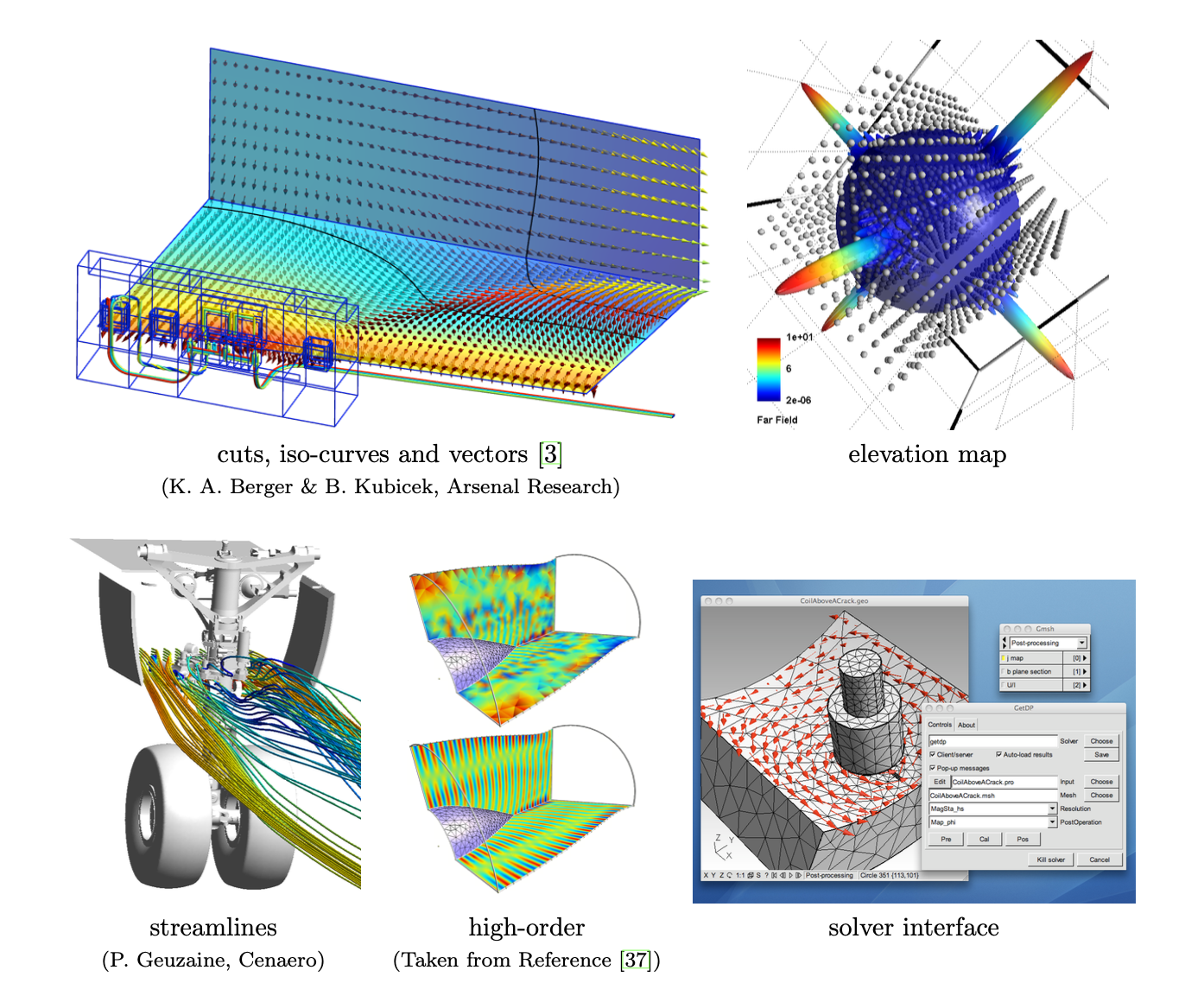
Figure 11: 来自求解器和后处理模块的一些图像.
8. Gmsh 中的后处理
后处理模块可以一次性加载、转换和显示多个后处理数据集 (称为“视图”), 以及几何和网格. 每个视图可以包含标量、矢量和张量数据的混合以及文本注释. 视图可以全局或单独操作 (每个视图在 GUI 中都有自己的按钮, 并且可以在脚本中通过其索引引用), 每个视图都拥有自己的一套显示选项. 在内部, 视图是一个抽象类, 可以访问各种底层表示, 从标准有限元代码中使用的基于节点的数据集到高阶、不连续的数据集, 例如在不连续 Galerkin 或有限体积求解器中使用的数据集 [37].
标量场由等值面或颜色图表示, 而矢量场由三维箭头或位移图表示 (见图13). 图形显示代码是使用 OpenGL 编写的, 所有表示在内部都存储为顶点数组以提高渲染性能.
显示选项是非破坏性的 (它们不会修改数据集), 并且可以动态更改. 这些选项包括例如选择绘图类型和要显示的等值面数量, 修改比例尺和颜色图的类型和范围, 或应用复杂的几何变换——基于函数表达式的坐标变化, 例如利用对称性或基于数据集中的值应用几何偏移.
除了非破坏性显示选项外, 后处理模块还提供了一个插件架构, 以便对视图进行破坏性修改. Gmsh 自带约三十个默认插件, 执行诸如计算截面、高程图和流线, 提取边界、组件和时间步, 应用微分算子, 计算特征值和特征向量, 或对点数据集进行三角剖分等操作.
所有的后处理功能都可以通过交互式或脚本语言访问, 这允许自动化所有操作, 例如创建动画. Gmsh 提供了大量的光栅输出格式, 以及用于使用 GL2PS [15] 进行高质量技术渲染的矢量输出, 这对于二维场景特别有用. 也可以使用离屏渲染 [32] 创建尺寸大于屏幕分辨率允许的光栅文件.
9. 展望和未来发展
在本文中, 我们介绍了 Gmsh 的整体架构及其一些特定功能. Gmsh 正在迅速发展, 近期计划了许多新的开发: 各向异性三维算法和更先进的边界层功能、并行网格划分、曲面重新参数化和高阶网格等等.
其中, 开发健壮的高阶网格生成程序至关重要. 事实上, 工程中的高阶方法已成为一个密集的研究领域, 然而, 在曲线网格生成领域所做的工作却很少. 这个问题远非微不足道: 将高阶顶点捕捉到几何上可能会导致单元变得无效, 必须实施复杂的网格解缠结程序以恢复网格的有效性.
与日益壮大的 Gmsh 用户和开发者开源社区一起, 我们相信我们正走在正确的轨道上, 可以在不妥协本文中提出的原始设计目标的情况下实现这些功能.
10. 致谢
作者衷心感谢法国电力公司 (EDF) 的财务支持. 我们也想感谢所有为 Gmsh 的开发、测试和调试做出贡献的人. 其中, 我们特别感谢 David Colignon 作为一位不知疲倦的 beta 测试者.
11. 参考文献
M. W. Beall and M. S. Shephard. A general topology-based mesh data structure. International Journal for Numerical Methods in Engineering, 40(9):1573-1596, 1997.
E. Bechet, J.-C. Cuillere, and F. Trochu. Generation of a finite element mesh from stereolithography (stl) files. Computer-Aided Design, 34(1):1-17, 2002.
K. A. Berger and B. Kubicek. Magnetic field of a 30kV/400V-substation. Private communication, Arsenal Research. Austria.
J.-C. Cuilliere. An adaptive method for the automatic triangulation of 3d parametric surfaces. Computer-Aided Design, 2:139-149, 1998.
Debian. Debian linux. http://www.debian.org.
G. Dhondt and K. Wittig. Calculix: A free software three-dimensional structural finite element program, 1998. http://www.calculix.de.
J. Dongarra. A set of level 3 basic linear algebra subprograms. ACM Transactions on Mathematical Software (TOMS), 16(1):1-17, 1990.
P. Dular and C. Geuzaine. GetDP: a general environment for the treatment of discrete problems, 1997. http://www.geuz.org/getdp/.
R. A. Dwyer. A simple divide-and-conquer algorithm for computing delaunay triangulations in o(n log log n) expected time. In Proceedings of the second annual symposium on Computational geometry, pages 276-284, 1986.
L. A. Freitag and C. Ollivier-Gooch. Tetrahedral mesh improvement using face swapping and smoothing. International Journal for Numerical Methods in Engineering, 40(21):3979-4002, 1998.
P. J. Frey. About surface remeshing. In 9th International Meshing Roundtable, 2000.
P.-L. George and H. Borouchaki. Delaunay Triangulation and Meshing: Application to Finite Elements. Hermes, 1998.
P.-L. George and P. Frey. Mesh Generation. Hermes, 2000.
P.-L. George, F. Hecht, and E. Saltel. Automatic mesh generator with specified boundary. Computer Methods in Applied Mechanics and Engineering, 92(3):269-288, 1991.
C. Geuzaine. GL2PS: an OpenGL to PostScript printing library, 2000. http://www.geuz.org/g12ps/.
C. Geuzaine and J.-F. Remacle. Gmsh: a finite element mesh generator with built-in pre- and post-processing facilities, 1996. http://www.geuz.org/gmsh/.
GNU. The GNU general public license, 1988. http://www.gnu.org/licenses/gpl.html.
R. Haimes. CAPRI: Computational analysis programming interface (a solid modeling based infra-structure for engineering analysis and design). Technical report, Massachusetts Institute of Technology, 2000.
F. Hecht. Bamg: Bidimensional anisotropic mesh generator, 2006. http://www.freefem.org/ff++.
D. Heller, P. M. Ferguson, and D. Brennan. Motif Programming Manual, volume 6A. O'Reilly, second edition, 1994.
B. Joe. GEOMPACK a software package for the generation of meshes using geometric algorithms. Adv. Eng. Software, 13:325-331, 1991.
J. Lambrechts, R. Comblen, V. Legat, C. Geuzaine, and J.-F. Remacle. Multiscale mesh generation on the sphere. Ocean Dynamics, 58:461-473, 2008.
P. Laug and H. Borouchaki. Blsurf-mesh generator for composite parametric surfaces-user's manual, 1999. Technical Report, INRIA, France.
J. R. Levine, T. Mason, and D. Brown. Lex & Yacc. O'Reilly, 1992.
X. Li. Mesh Modification procedure for General 3-D Non-Manifold Domains. PhD thesis, Renselear Polytechnic Indtitute, 2003.
X. Li, J.-F. Remacle, N. Chevaugeon, and M. S. Shephard. Anisotropic mesh gradation control. In 13th International Meshing Roundtable, 2004.
A. Liu and B. Joe. Relationship between tetrahedron shape measures. BIT Numerical Mathematics, 34(2):268-287, 1994.
H. Lo and W. X. Wang. Generation of anisotropic mesh by ellipse packing over an unbounded domain. Engineering with Computers, 20(4):372-383, 2005.
M. Muuss. BRL-CAD, 1984. Army Research Laboratory.
C. F. Ollivier-Gooch. GRUMMP generation and refinement of unstructured, mixed-element meshes in parallel, 1998. http://tetra.mech.ubc.ca/GRUMMP/.
F. Ortega. GMV: The general mesh viewer, 1996. http://www-xdiv.lanl.gov/XCM/gmv/GMVHome.html.
B. Paul. The Mesa 3D graphics library, 1995. http://www.mesa3d.org/.
P. P. Pebay and T. J. Baker. Analysis of triangle quality measures. Mathematics of Computation, 72(244):1817-1839, 2003.
L. Piegl and W. Tiller. The Nurbs Book. Springer, 1997.
S. Rebay. Efficient unstructured mesh generation by means of delaunay triangulation and bowyer-watson algorithm. Journal of Computational Physics, 106:25-138, 1993.
J.-F. Remacle, X. Li, M. S. Shephard, and J. E. Flaherty. Anisotropic adaptive simulation of transient flows using discontinuous galerkin methods. International Journal for Numerical Methods in Engineering, 62(7):899-923, 2005.
J.-F. Remacle, E. Marchandise, N. Chevaugeon, and C. Geuzaine. Efficient visualization of high order finite elements. International Journal for Numerical Methods in Engineering, 69(4):750-771, 2007.
Open CASCADE S.A.S. Open cascade. http://www.opencascade.org.
J. Schöberl. Netgen, an advancing front 2d/3d-mesh generator based on abstract rules. Comput. Visual. Sci., 1:41-52, 1997.
W. Schroeder, K. Martin, and B. Lorensen. The visualization toolkit. Prentice Hall, 1998.
SDRC. I-DEAS master series, 1993.
M. Segal and K. Akeley. The OpenGL graphics system: A specification. Technical report, Silicon Graphics Computer Systems, 1992.
J. R. Shewchuk. Robust Adaptive Floating-Point Geometric Predicates, May 1996.
J. R. Shewchuk. Triangle: Engineering a 2D Quality Mesh Generator and Delaunay Triangulator. In Applied Computational Geometry: Towards Geometric Engineering, volume 1148 of Lecture Notes in Computer Science, pages 203-222. Springer-Verlag, May 1996.
K. Shimada, A. Yamada, and T. Itoh. Anisotropic triangular meshing of parametric surfaces via close packing of ellipsoidal bubbles. In 6th International Meshing Roundtable, pages 375-390, 1997.
H. Si. Tetgen a quality tetrahedral mesh generator and three-dimensional delaunay triangulator, 2004. http://tetgen.berlios.de/.
Siemens PLM Software. Parasolid. http://www.parasolid.com.
B. Spitzak. FLTK, the fast light tool kit, 1998. http://www.fltk.org.
Paul S. Strauss. IRIS Inventor, a 3D graphics toolkit. ACM SIGPLAN Notices, 28(10):192-200, 1993.
B. Stroustrup. The C++ Programming Language. Addison-Wesley, 1997.
Dassault Systèmes. Catia. http://www.3ds.com.
G. V. Vaughan and T. Tromey. GNU Autoconf, Automake and Libtool. New Riders Publishing, 2000.
S. Vavasis. QMG: mesh generation and related software, 1995. http://www.cs.cornell.edu/home/vavasis/qmg-home.html.
S. Vinoski. CORBA: integrating diverse applications within distributed heterogeneous environments. IEEE Communications Magazine, 35(2):46-55, 1997.
D. F. Watson. Computing the n-dimensional delaunay tessellation with application to voronoï polytopes. the Computer Journal, 24(2):167-175, 1981.
N. P. Weatherill. The integrity of geometrical boundaries in the two-dimensional delaunay triangulation. Communications in Applied Numerical Methods, 6(2):101-109, 1990.
M. A. Yerry and M. S. Shephard. Automatic three-dimensional mesh generation by the modified-octree technique. International Journal for Numerical Methods in Engineering, 20(11):1965-1990, 1984.